Поскольку CD²=AC²-AD² и CD²=AD×BD, то AC²-AD²=AD×BD.
AC у нас есть, это 15 см, нет AB. AB у нас будет x, поэтому AD=x-16 (BD равно 16, исходя из условия).
Решаем уравнение:
15²-(x-16)²=(x-16)×16
225-x²+32x-256=16x-256
Перенесём всё в одну половину уравнения:
225-x²+32x-256-16x+256=0
-x²+16x+225=0
Умножим на -1 ради удобства:
x²-16x-225=0
Ищем дискриминант:
D=256+225*4=1156
Ищем x:
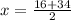
x=25 (см). Мы нашли гиппотенузу AB.
Отсюда:
1)AD=25-16=9 (см)
2)Hc²=9*16=144, Hc=12 (см)
3)BC²=625-225=400, BC=20 (см)
4)Pabc=20+25+15=60 (см)
5)Sabc=0.5×15×20=150 (см²)
на первой 10
на второй 4
Пошаговое объяснение:
на 6 человек больше -- +6 например 9 больше 3 на 6
выражением
(п. - пассажиры)
первый
1)14+6=20(п.) - количество людей зашедших на первой остановке*2
2)20: 2=10(п.) - зашло на первой
3)14-10=4(п.) - зашло на второй
второй
1)14-6=8(п.) - количество людей зашедших на 2 остановке*2
2)8:2=4(п.) - зашло на второй остановке
3)14-4=10(п.) - зашло на первой остановке
уравнением
Примем количество пассажиров вошедших на первой остановке за х , а на второй остановке за у.
1. Составим два уравнения на основании условия:
1) х + у = 14,
2) х = у + 6.
2. Подставим значение х из второго уравнения в первое и определим у:
х + у = 14,
(у + 6) + у = 14,
2·у + 6 = 14,
2·у = 14 - 6,
2·у = 8,
у = 8:2,
у = 4 пассажира - вошли на 2-й остановке.
3. Вычислим количество пассажиров, вошедших на первой остановке:
х = у + 6 = 4 + 6 = 10.
ответ: на 1-й остановке зашло 10 пассажиров, на 2-й - 4.
Решение задания приложено