Пошаговое объяснение:
1.
y = x/2; y = 0
x=2
z=xy; z=0
x = 2 и у = х/2 - это плоскости, параллельные Оz, проходящие через Ох и Оу.
z = ху - это седло, проходящее через оси координат Ox, Oy
т.к. поверхность x = 2 должна участвовать в формировании области, у поверхности z = xy надо брать ту часть, где x > 0.
и еще z = xy и z = 0 ⇒ x = 0; y =0
проекцией области на плоскость xOy будет треугольник
, где
0 ≤ x ≤ 2, y ≤ x/2.
вот, получили пределы интегрирования
проекцией области на плоскость xOy будет треугольник
: 0 ≤ x ≤ 1, y ≤ x/2. для каждой точки (x, y) ∈ точка (x, y, z) будет в
области при 0 ≤ z ≤ xy.
вот, получили пределы интегрирования
0 ≤ x ≤ 2
0≤y ≤ x/2
0 ≤ z ≤ xy
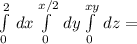
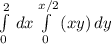
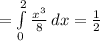
2.
формула длины дуги
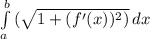
у нас f'(x) = √x
длина дуги
![\int\limits^4_0 {\sqrt{1+x} } \, dx = \left[\begin{array}{ccc}u=1+x\\du = dx\\\end{array}\right] =](/tpl/images/1357/4350/5274b.png)
[ так же пересчитаем пределы интегрирования нижний u = 1+0 = 1, верхний u = 1+4 = 5] =
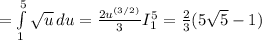
60,80
Пошаговое объяснение:
Предположим, что одновременно музыкой и спортом занимаются х человек. Тогда тех, кто занимается только музыкой, 3х человек (так как их по условию в 3 раза больше). А учащихся, занимающихся толко спортом, 4х человек (так как их по условию в 4 раза больше). По условию, музыкой или спортом занимаются 160 человек. Составим уравнение:
3х + х + 4х = 160,
8х = 160,
х = 160 : 8,
х = 20.
Таким образом, учащихся, занимающихся одновременно и музыкой, и спортом, 20 человек. Тогда только музыкой занимаются 3*20 = 60 человек, только спортом 4*20 = 80 человек.
Выяснили, что есть 20 учащихся, которые занимаются и музыкой и спортом, и ещё 60 учащихся-музыкантов. Значит, общее количество учащихся, которые занимаются музыкой: 20 + 60 = 80 человек (число элементов множества А).
Всё также есть 20 человек, которые занимаются и музыкой, и спортом, и ещё 80 учащихся-спортсменов,. Значит, общее количество учеников, которые занимаются спортом: 20 + 80 = 100 человек (число элементов множества В).
Проверка:
60 + 20 + 80 = 160
160 = 160.
ответ: число элементов множества А составляет 60, множества В - 80.