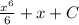
Пошаговое объяснение:
ну согласно свойствам интегралов, коих множество и изучить их надо, чтобы понимать и легко решать, данный интеграл можно представить следующим образом:

это уже сумма двух табличных интегралов.
Заглядываем в таблицу интегралов, которую Вы должны выучить наизусть как таблицу умножения и уже должна быть выучена наизусть таблица производных.
Это опять же, если Вы хотите легко и хорошо решать такие примеры.
В таблице находим похожий интеграл:
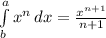
подставляем наши значения по аналогии в данный табличный пример и получаем:
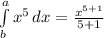
и со вторым выражением также:
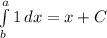
Вот и решили, осталось записать всё в одну строчку:
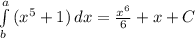
8
Пошаговое объяснение:
Сумма каждых 6 последовательных чисел равна 50.
Тогда сумма первых 6 чисел: x1+x2+x3+x4+x5+x6=50.
Сдвинемся на одно число: x2+x3+x4+x5+x6+x7=50. В таком случае x7 должно быть равно x1, иначе равенство не выполнится. Продолжим движение до конца круга: x8=x2, x9=x3, x10=x4, x11=x5, x12=x6, x13=x7=x1, x14=x8=x2, x15=x9=x3. Числа закончились, но пятнадцатым числом оказалось не шестое, а третье, значит, можно продолжить движение. Тогда получается, что x1=x10=x4, x2=x11=x5, а x3=x12=x6. Из этого узнаем, что x1=x4, x2=x5, а x3=x6.
Можно составить уравнение:
x1+x2+x3+x1+x2+x3=50
x1+x2+x3=25
Первое и третье число даны в условии: 7 и 10. Подставляем их и находим второе, стоящее между ними:
7+x2+10=25
17+x2=25
x2=8
Следовательно, под карточкой число 8