в 3 номере под а):
показатели корней разные (12 и 6), мы можем получить одинаковые, умножив показатель 6 на 2, поэтому и подкоренное выражение домножаем на 2:
было: √6ой степени из 5⁵, стало: √12ой степени из 5¹⁰
то же самое в номере 3 под б):
показатели корней разные (квадратный корень из 3 и кубический корень из 9), мы можем получить одинаковые, домножив квадратный корень на 3 (чтобы получить 6) и кубический корень на 2 (чтобы получить 6), поэтому и подкоренные выражения домножаем на 2:
было: √2ой степени из 3, стало: √6ой степени из 3³ и второй множитель: было: √3ей степени из 9, стало: √6ой степени из 9²
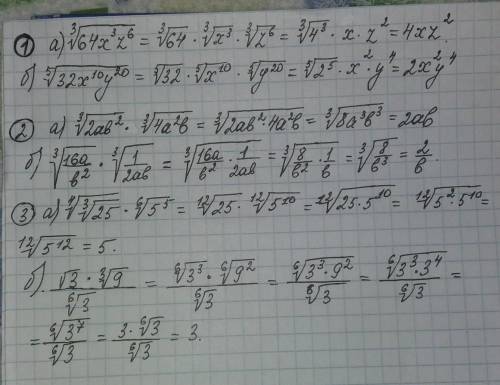
830 и 83
Пошаговое объяснение:
По условию одно из чисел заканчивается 0 и это большее число , поскольку при зачеркивании 0 мы получаем второе число . Запишем наше выражение в виде :
* * 0
* *
9 1 3
3-0 = 3 , значит число единиц во втором числе , и число десятков в первом числе равно 3 ( поскольку по условию они одинаковые)
* 3 0
* 3
9 1 3
Найдем число , которое в сумме с 3 оканчивается на 1
3+8= 11 , значит число десятков во втором числе и число сотен в первом числе равно 8 ( одинаковые по условию)
8 3 0
8 3
9 1 3
верно
Искомые числа :
830 и 83
1). -(m - 38) + (412 + m) =450
2). -(243 + X-b) - (243 + b-x) =-486
3). -(153-x+ a) - (x-a- 253) =100
4). -(a-x) - (51 + х) +a-51 =-202
5). (b-x) - (a-x) + (a-b) =0
6). -(a + 33) - (x-a) - 33 +х =-66
7). (243 + 11) - (b+ 243) + (0-11) =-b
8). (153-x+a) - (х - 153 - a) - а =-2x+a
9). - (а - 121) - (1-a) - (21 - а)=99+a
Пошаговое объяснение: