 .
.
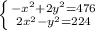
Пошаговое объяснение:
2 C самого начала обратим внимание на то, что предложенную задачу можно выполнить как формул, так и логических рассуждений. B данном случае воспользуемся вторым вариантом.
Если сделать допущение, что нет никаких критериев выбора (все 8 учеников условно равны), то первого ученика мы будем выбирать из 8 школьников (т.e. есть 8 вариантов выбора). Соответственно, второго будем выбирать из 7, a третьего - из 6. Тогда всего ответ: всего Пары (n; m) и (m; n) это одна пара.
С (10; 2) = 10 / 2 8=45
4
Всего тетрадей 8+4 = 12 тетрадей всего в папке. Вероятность того, что вытащили линеечную тетрадь в первый раз равна 8/12 = 2/3. формула есть такая. вероятность равна частному требуемых исходов на всевозможные
во второй раз если выбирать то теперь выбирается из 11 тетрадей. и тетрадок в линейку уже не 8, а 7
вероятность будет 7/11
А общая вероятность того, что обе тетрадки в линию равна произведению вероятностей
(2/3)*(7/11) = 14/33 = приблизительно = 42%
5
Всего всевозможных исходов: 6+8+5=19 из них 8 благоприятные исходы.
m = 8
n = 19
Искомая вероятность: P = m/n = 8/19
V увел. = 4/3 • п(2R)^2 - объём шара, с радиусом , увеличенным вдвое.
Масса шара прямопропорциональна его объему.
M увел. : М исх. = V увел. : V исх.
M увел. : М исх. = 4/3 • п(2R)^2 : (4/3 • пR^2)
M увел. : М исх. = (2R)^2 : (R^2)
M увел. : М исх. = 4(R^2) : (R^2)
M увел. : М исх. = 4
М увел. = 4 • М исх.
М увел. = 4 • 360
М увел. = 1440 г - масса шара вдвое большего радиуса.
ответ: 1440 г.