Обозначим скорость лодки как х, а скорость реки как y.
Нам известно, что путь S вычисляется по формуле S=v*t
Найдем сначала путь который шляпа за 15 минут
Sш=15*y Это путь который пройдет шляпа за 15 минут.
Найдем путь который пройдет лодка за 15 минут, т.к плывем против течения, то из скорости лодки вычитается скорость течения, значит скорость лодки против течения будет x-y. Теперь найдем путь:
Sл=15*(x-y)
Теперь найдем расстояние между шляпой и лодкой через 15 минут
Sобщ=15*(x-y)+15*y=15*x
Теперь рассматриваем момент, когда лодка плывет по течению. Ее скорость будет x+y (скорость лодки плюс скорость реки)
Так как шляпа плывет со скоростью реки и лодка плывет с собственной скоростью+скорость реки, то мы можем свести задачу к другой:
Найти время за которое лодка проплывет путь Sобщ при скорости x.
Это можно сделать потому что шляпа будет удаляться со скоростью у, а лодка будет к ней приближаться со скоростью х+у, значит можно считать что шляпа стоит, а лодка плывет к ней, но уже со скорость х.
Найдем теперь это время. Из формулы S=vt получаем, что t=S/v
Путь нам известен он равен Sобщ, скорость лодки нам тоже известна она равна х.(почему смотри выше)
Найдем время: 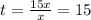 минут
минут
ответ: Лодка догонит шляпу через 15 минут, после того, как поплывет по течению
№1. Пусть на старом прессе изготавливают 300 деталей за х часов, тогда его за 1 час на нем делают 300/х деталей. На новом 300 деталей делают за х-3 часа, т.е. за 1 час делают 300/х деталей. Теперь они работают одновременно:
1) 5 старых за 1 час - 1500/х деталей, 2) 2 новых за 1 час - 600/(х-3) детали.
Вместе это по условию 600 деталей. Уравнение: 1500/х + 600/(х-2) = 600
После упрощения: 2x^2 -13x + 15 = 0, x = 1,5 - не подходит по условию, так как тогда
х - 3 <0; x = 5. Значит, тогда старый за 1 час сделает 300/5 = 60 деталей, а новый
300/(5 - 3) = 150 деталей
№2. 1) x^2 - 5x + 7 > 0, D < 0. Значит, этот трехчлен > 0 при любом х
2) lg(x^2 - 5x +7) >= 0, x^2 -5x + 7 >= 10^0, x^2 - 5x +7 >= 1,
x^2 - 5x + 6 >= 0, метод интервалов: x^2 - 5x +6 =0, x=2; 3
наносим на числовую прямую найденные значения х и расставляем знаки трехчлена.
Получим: на промежутке (-беск; 2] трехчлен >= 0; на [2; 3] <=0;
на [3; +беск) >=0. Нам нужны промежутки, где >=0, т.е. ответ
(-беск; 2] и [3; +беск)
Пошаговое объяснение:
Дано: y =0,5*x²+-3*x+0 - квадратное уравнение.
Положительная парабола - ветви вверх.
Пошаговое объяснение: a*x² + b*x + c = 0 Вычисляем дискриминант - D.
D = b² - 4*a*c = -3² - 4*(0,5)*(0) = 9 - дискриминант. √D = 3.
Вычисляем корни уравнения.
x₁ = (-b+√D)/(2*a) = (3+3)/(2*0,5) = 6/1 = 6 - первый корень
x₂ = (-b-√D)/(2*a) = (3-3)/(2*0,5) = 0/1 = 0 - второй корень
6 и 0 - корни уравнения - точки пересечения с осью ОХ.
Минимальное значение по середине корней при Х=3
У(3) = 1/2*9 - 3*3 = 4.5 * 9 = - 4.5
Таблица с точками для построения графика - в приложении.
Рисунок с графиком в приложении.