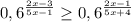
Показательная функция с основанием (0 <0,6 <1) убывающая, значит большему значению функции соответствует меньшее значение аргумента
Это означает, что в неравенстве между показателями степеней знак меньше:
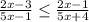
Получили дробно- рациональное неравенство.
Переносим выражение справа в левую часть
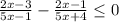
Приводим к общему знаменателю и получаем неравенство
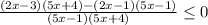
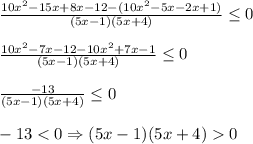
Знаменатель дроби не должен равняться 0, поэтому неравенство строгое.
Решение неравенства x < -4/5 или x>1/5
Интервалов два:
(-∞;-4/5) U (1/5;+∞)
Наименьшее целое положительное х=1
В ответ не вошли числа принадлежащие
[-4/5;1/5]
Далее непонятен вопрос, сумму каких чисел надо найти:
целых положительных?
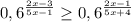
Показательная функция с основанием (0 <0,6 <1) убывающая, значит большему значению функции соответствует меньшее значение аргумента
Это означает, что в неравенстве между показателями степеней знак меньше:
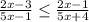
Получили дробно- рациональное неравенство.
Переносим выражение справа в левую часть
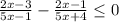
Приводим к общему знаменателю и получаем неравенство
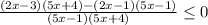
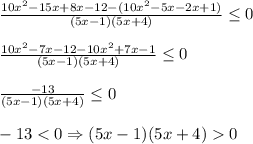
Знаменатель дроби не должен равняться 0, поэтому неравенство строгое.
Решение неравенства x < -4/5 или x>1/5
Интервалов два:
(-∞;-4/5) U (1/5;+∞)
Наименьшее целое положительное х=1
В ответ не вошли числа принадлежащие
[-4/5;1/5]
Далее непонятен вопрос, сумму каких чисел надо найти:
целых положительных?
Объяснение:
Поиск экстремумов по первой производной.
9. Первая производная. Y'(x) = -3*x² -18*x + (0) = 0
Корни Y'(x)=0. Х =0 Х= -6 - за областью определения.
Производная отрицательна между корнями - функция убывает.
10. Локальные экстремумы.
Максимум - Ymax( 0) =3. Минимум - Ymin(3) = -105