70-(59-30) наибольшее из 3-х выражений
Пошаговое объяснение:
Немного преобразуем 1-е выражение
70 - (59 - 30) = (70 - 59) + 30
И теперь сравним его со 2-м выражением
Сначала сравним скобки
70 > 67 а 59 < 60
Когда в скобке в 1-м выражении уменьшаемое больше, а вычитаемое меньше, чем в скобке во 2-м выражении, то, конечно, разность в скобке 1-го выражения больше, чем разность в скобке 2-го выражения. Затем к скобкам прибавляется одно и то же число 30. Следовательно, 1-е выражение больше 2-го.
Теперь сравним 1-е выражение и 3-е
(70 - 59) + 30 и (6 -4) + 5
Очевидно, что (70 - 59) > 10, a (6 - 4) < 10, поэтому
(70 - 59) > (6 - 4)
Также и 30 > 5, поэтому 1-е выражение больше 3-го
Итак, 70-(59-30) наибольшее из 3-х выражений
x² + y² + 6x + 8y + 24 = 0
x² + 6x + 9 + y² + 8y + 16 = 1
(x+3)² + (y+4)² = 1
Это уравнение окружности с центром (-3;-4) и радиусом R = 1.
Дополнительно построим окружность с центром (-3;-4) и радиусом R = 5 (для того чтобы эта окружность проходила через точку начала координат, будет проще найти расстояния).
Расстояние от точки А до точки С равно 1, поскольку это есть радиус маленькой окружности, а расстояние от точки А до точки В равно 5. Следовательно, искомое расстояние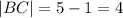
ответ: 4.