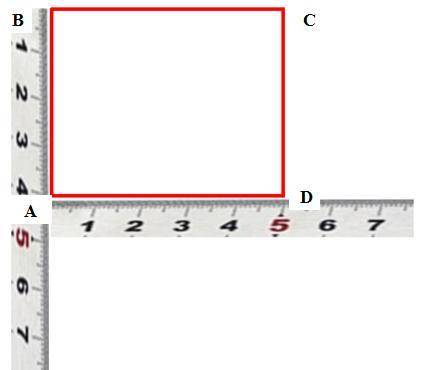
С линейки построим и обозначим вершины через ABCD (см. рисунок 1).
1. Вычислим периметр прямоугольник со сторонами AB=4 см и AD=5 см по формуле периметра:
P=2·(AB + AD)=2·(4 см + 5 см)= 2·9 см= 18 см
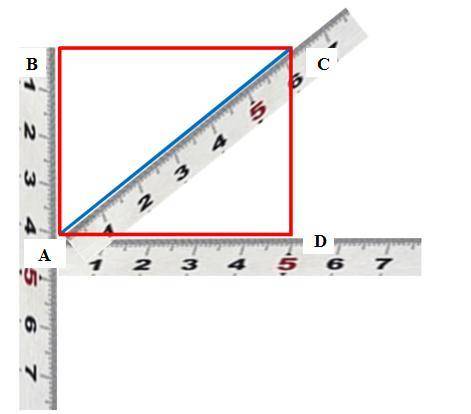
2. Проведем диагональ AC прямоугольника и измерим её (см. рисунок 2). Длина AC равна приблизительно 6,4 см. Тогда, так как 5 < 6,4, то большая сторона прямоугольника AD < AC.
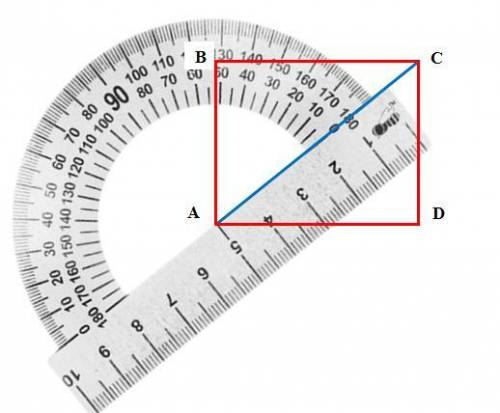
3. С транспортира измерим угол между диагональю и меньшей стороной прямоугольника (см. рисунок 3). Угол составляет приблизительно 52°.
f'(x) = 3x^2 - 8x +4
f'(x) = 0
3x^2 - 8x +4 = 0
x = 2/3; x = 2
Xmax = 2/3
Xmin = 2
Возрастает на промежутках от минус бесконечности до 2/3 и от 2 до плюс бесконечности
У бывает на промежутке от 2/3 до 2