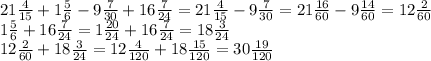
Мне очень сложно отвечать. Вложение не работает. конечно. то, что Вы изобразили графиком, извините. далеко от идеала, но и я построить не смогу. т.к. с вложением проблема. Оттолкнемся от того, что имеем. Нам надо найти наибольшее и наименьшее значение функции на указанных промежутках, промежуток этот из области определения. т.е. это х∈ [-2;6]
Если Вы знакомы с производной. то поступают так.
производная равна -0.2*2х=0, если х=0, эта точка входит в отрезок [-2;6]
затем находят значение функции в точках 0, -2, 6. выбирают из них самое большое и самое маленькое.
у(0)=-0.2*0=0-наибольшее.
у(-2)=-0.2*4=-0.8
у(6)=-0.2*36=-7.2 -наименьшее
б) берем отрезок [-5;5]
ноль опять попадает в этот отрезок.
у(0)=0-наибоьшее.
У(-5)=-0.2*25=-5-наименьшее
у(5)=-0.2*25=-5- наименьшее
Вообще наибольшее или наименьшее значение функции- это значение у. а промежуток, или отрезок- это значения х.
Окончательно -- надеюсь. Вы поняли. кто прав.
128 = 2⁷; 80 = 2⁴ · 5
НОД (128; 80) = 2⁴ = 16 - наибольший общий делитель
28 = 2² · 7; 55 = 5 · 11
НОД (28; 55) = 1 - наибольший общий делитель
Числа 28 и 55 взаимно простые, так как у них нет общих делителей, кроме единицы
120 = 2³ · 3 · 5; 15 = 3 · 5
НОД (120; 15) = 3 · 5 = 15 - наибольший общий делитель
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
25 = 5²; 60 = 2² · 3 · 5
НОК (25; 60) = 2² · 3 · 5² = 300 - наименьшее общее кратное
14 = 2 · 7; 165 = 3 · 5 · 11
НОК (14; 165) = 14 · 165 = 2310 - наименьшее общее кратное
Числа 14 и 165 взаимно простые, так как у них нет общих делителей, кроме единицы
180 = 2² · 3² · 5; 12 = 2² · 3
НОК (180; 12) = 2² · 3² · 5 = 180 - наименьшее общее кратное
1) 21 4/15 + 1 5/6 = 21 8/30 + 1 25/30 = 22 33/30
2) 22 33/30 - 9 7/30 = 13 26/30
3) 13 26/30 + 16 7/24 = ( 13 + 16 ) + ( 26/30 + 7/24 ) = 29 + 13/15 + 7/24 = 29 + 104+35/120 = 29 + 139/120 = 29 + 1 19/120 = 30 19/120