Пошаговое объяснение: в приложении
Построение раскроев
Пусть даны n типов заготовок с номерами 1,...,n и длинами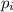 
, а исходные стержни имеют длину 
.
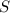В начале поиска полагаем i=1
1. Ищем максимально возможное число заготовок типа i. Оно, очевидно, равно ![N=\left[\dfrac{S}{p_i}\right]](/tpl/images/1537/7845/f1eeb.png)
, где [х] - целая часть числа x.
2. Ищем длину незадействованной части стержня. Она, очевидно, равна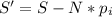 
3. Если существует заготовка с номером, большим i, и длиной, меньшей S', и решаем аналогичную задачу для стержня длиной S' и заготовок с номерами i+1,...,n. Иначе пункт 4.
4. Получен вариант раскроя. Записываем число отходов.
5. Если N≥1 и i≠n, уменьшаем N на 1, и решаем аналогичную задачу для стержня длиной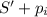 
и заготовок с номерами i+1,...,n
Переместительное свойство сложения: От перестановки слагаемых сумма не меняется.
Сочетательное свойство сложения: Чтобы к сумме двух чисел прибавить третье число можно к первому числу прибавить сумму второго и третьего числа.
Переместительное свойство умножения: От перестановки множителей произведение не меняется.
Сочетательное свойство умножения: Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.
Пошаговое объяснение: