Найдем сначала общее решение соответствующего однородного дифференциального уравнения:
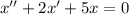
Используя замену 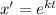 , получим характеристическое уравнение
, получим характеристическое уравнение
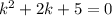
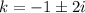
Общее решение однородного дифференциального уравнения:
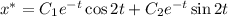
Рассмотрим функцию: 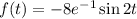 . Здесь
. Здесь 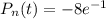 откуда
откуда 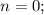 и
и 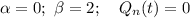 . Сравнивая α, β с корнями характеристического уравнения, частное решение будем искать в виде:
. Сравнивая α, β с корнями характеристического уравнения, частное решение будем искать в виде:
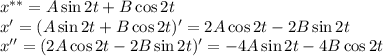
Подставляем в исходное дифференциальное уравнение:
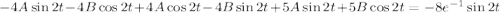
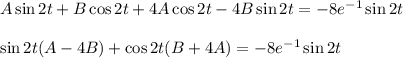
Приравниваем коэффициенты при cos2x и sin2x, получаем систему:
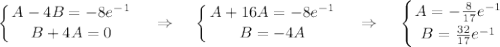
Общее решение линейного неоднородного дифференциального уравнения:
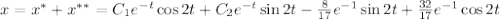
Осталось решить задачу Коши, подставляя начальные условия
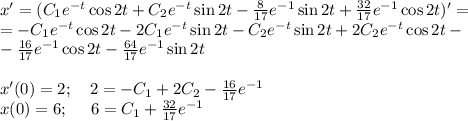
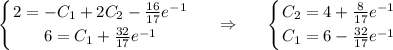
Частное решение задачки Коши:
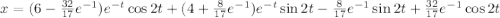
Во время строительства ГЭС особенно большим будет перемещение грязи и отложений вниз по течению от места возведения станции. Земляные работы и проходка туннеля могут привести к значительному ухудшению качества воды, что вызовет дополнительные проблемы. Склад воды;объект, существенно изменяющий исходное качество речной воды (улучшая или ухудшая ее показания);акватория, используемая водным транспортом, лесосплавом, рыбным хозяйством, в целях рекреации;объект, позволяющий в ряде районов значительно увеличить использование земельных ресурсов (ирригация, борьба с наводнениями, территориальное перераспределение стока);объект, вносящий заметные изменения в природу и хозяйство речных долин, дельт, озер, приустьевых участков морей.