Обозначим длину прямоугольника как а, ширину прямоугольника как b, и диагональ как c.
Рассмотрим ΔABC: ∠B=90° ⇒ ΔABC - прямоугольный; a,b - катеты, c - гипотенуза
т. Пифагора гласит:
a² + b² = c²
a² + b² = 13²
a² + b² = 169
А площадь прямоугольника находится по формуле:
S = a * b
a * b = 60
Составим систему уравнений и решим методом подстановки.

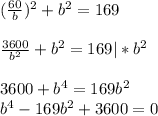
Вводим новую переменную.
b² = t - новая переменная.
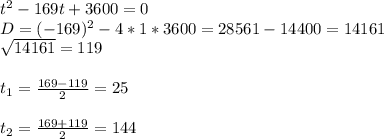
b² = t
b² = 25 или b² = 144
b₁ = 5; b₂=-5; b₃=12; b₄=-12
Т.к. сторона не может быть отрицательна, то -5 и -12 не подходят.
a * b = 60
a₁ * 5 = 60
a₁ = 12
a₂ * 12 = 60
a₂ = 5
⇒ Стороны прямоугольника равны 5 см и 12 см.
ответ: 5 см; 12 см

5 и 12
Пошаговое объяснение:
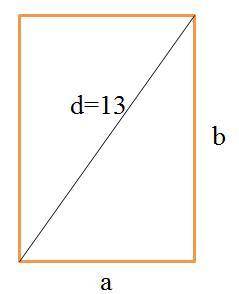
Пусть стороны прямоугольника a и b, диагональ d. Площадь прямоугольника равна: S = a · b. По условию a · b = 60, а диагональ d = 13.
Диагональ делит прямоугольник на два прямоугольных треугольника и поэтому верна теорема Пифагора: d² = a² + b².
На основе условий задачи получаем систему уравнений:
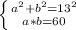
Второе уравнение умножим на 2 и прибавим к первому:
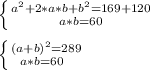
a и b стороны прямоугольника и поэтому a+b>0:
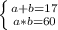
Решаем систему методом подстановки:
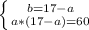
a²-17·a+60=0
D=(-17)²-4·1·60=259-240=49=7²
a₁=(17-7)/2=10/2=5, тогда b₁ =17-5=12
a₂=(17+7)/2=24/2=12, тогда b₂ =17-12=5.
Отсюда, ответом будут 5 и 12.
Мартышка Зося, Тося, Бося и Дося - хотят стать участниками чемпионата по бальным танцам. Но проблема, нужен кавалер. На пришли Артур, Картер и Дактур. Победить в чемпионате может только одна пара. Сколько возможных вариантов пар-победительниц можно составить?
Зося, Тося, Бося, Дося - 4 мартышки.
Артур, Картер, Дактур - 3 обезьяны.
Соответственно можно 3 обезьяны перемножить на 4 мартышки и получится 12 вариантов пар-победительниц.
ответ: 12 вариантов пар-победительниц.Посчитаем пары:
Зоя с Артуром, Картером, Дактуром - 3 возможные пары-победительницы;
Тася с Артуром, Картером, Дактуром - 3 возможные пары-победительницы;
Бося с Артуром, Картером, Дактуром - 3 возможные пары-победительницы;
Дося с Артуром, Картером, Дактуром - 3 возможные пары-победительницы;
Итог: 3 + 3 + 3 + 3 = 6 + 6 = 12 вариантов пар-победительниц.
ответ: 12 вариантов пар-победительниц.