1) (5/7*7/3*5/6-1): (1-7/8*8/5*3/14)=(35/21*5/6-1):(1-56/40*3/14)=(175/126-1):(1-168/560)=(175/126-126/126): (560/560-168/560)=49/126:392/560=49*560/126*392=27440/49392= 1715/ 3087
2) (127/15-15/4+22/5-487/60): (17/4-11/4) =( 508/60-225/60+264/60-487/60):6/4=60/60: 6/4= 4/6=2/3
3) (21/13*13/42+40/7:8/21):(65/8+7/2)= (273/546+40*21/7*8):(65/8+28/8)=
(273/546+840/56):37/8= (273/546+8190/546):37/8= 8463/546 =155/10:37/8=155*8/370=1240/370=124/37=3 13/37
4) 13/5:91/15+15/14-112/73*(40/7-81/16)=
А)640/16-81/16=559/16
62608/1168=15652/292=3913 /73
195/455 + 3913/73= 14235 /33215+1780415/33215 =1794650/33215=54целых208/6643
Пошаговое объяснение:
Сумма цифр числа (n-1) равна
41 + 9•kгде k - количество нулей, стоящих на конце числа n
Пошаговое объяснение:
Оу! попробуем.
Итак, есть некое число
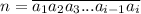
причем такое, что сумма его цифр равна 42.
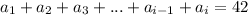
Обратим внимание, что ноли на конце этого числа n не оказывают влияния на сумму его цифр.
При вычитании единицы из n запись числа может принять следующие варианты:
а)
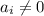
Уменьшается последняя цифра числа на единицу, остальные цифры не изменяются. Сумма цифр будет следующей:
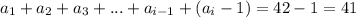
б)
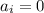
Сумма цифр будет выглядеть:
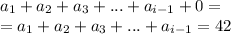
так как ноли на конце этого числа n не оказывают влияния на сумму его цифр.
Последняя цифра обращается в "9", предыдущая цифра уменьшается на единицу. Сумма цифр будет следующей:
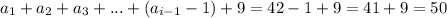
в) Несколько последних цифр (пусть, k цифр)- нули.
Число можно представить как
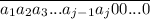
где а(j) - крайняя справа отличная от нуля цифра.
Сумма цифр будет выглядеть:
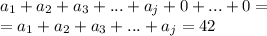
Количество нулей в этой записи равно k шт.
При вычитании единицы все эти нули на конце числа превращаются в "9". Девяток будет ровно столько же, сколько было нулей, т.е. k шт.
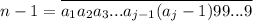
Сумма цифр для n-1 будет равна:
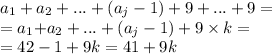
ОБОБЩЕНИЕ:
Все случаи можно отобразить одной формулой:
Сумма цифр числа
(n-1)
равна
41 + 9•kгде k - число нулей, стоящих на конце числа n
ответ: 23
пошаговое объяснение: