Всего- 65 км за 3 дня
В первый и второй день-47 км
Во второй и третий день - 40 км
Сколько в каждый день-?км
1)65-47=18 км- проехали в третий день
2)65-40=25 км- проехали в первый день
3)65-(25+18)=22 км- проехали во второй день
ответ: 25 км, 22 км,18 км
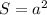
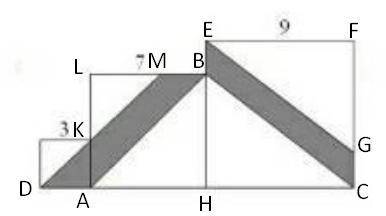
Площадь наименьшего квадрата - 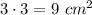
Среднего - 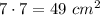
Большего - 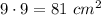
Диагональ меньшего квадрата обозначим за d, по формуле
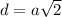
Где а - сторона, находим диагональ
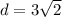
Первая часть "полосы" пересекает оба квадрата, поэтому обозначим её за S₁ ;
Во втором квадрате, в левом верхнем углу, можем заметить треугольник, в приложении он обозначен как KLM. Найти его гипотенузу не составит трудностей: сторона LM = 7 - 3 = 4 см; KL = 4 см, следовательно, гипотенуза (KM) равна 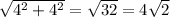
По упомянутому выше факту, мы видим, что "полоса" пересекает оба квадрата, значит стороны можно сложить
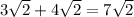
Нам известно две стороны параллелограмма (DM = AB), чтобы найти его площадь, нужно перемножить эти две стороны между собой и произведение умножить на синус угла между ними; так как в квадрате все углы по 90°, AB - диагональ, а значит, биссектриса, то угол между сторонами равен 45°. Значит,

Площадь второй части "полосы" обозначим за S₂;
Рассмотрим треугольник ABC:
AC = 7 + 9 = 16 см
BH - высота, = 7 см
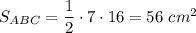
Так как ΔABH занимает ровно половину второго квадрата, то его площадь равна
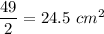
Тогда, ΔBHC = 56 - 24,5 = 31,5 см²
Рассмотрим треугольники EFG и BHC:
EF = HC (по усл.)
BH = FG (9 - 2 = 7 см)
⇒ ΔEFG = ΔBHC по 2 катетам
Из этого следует, что ΔEFG = ΔBHC = 31,5 см²
Вспоминаем, что в начале нашли площадь самого большого квадрата - 81 см²;
А значит,
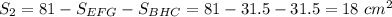
Итоговая площадь всей закрашенной части -
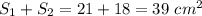
ответ: 39 см²
І
} 47км
ІІ } 65км
} 40км
ІІІ
1) 65-40=25(км) - за Ідень
2) 47-25=22(км) - за ІІ день
3) 40 - 22 = 18(км) - за ІІІдень
ответ: 25км, 22км и 18км проехали отец с сыном.