ответ: 4) S=12, 5) 3*y²-2*x³-3=0.
Пошаговое объяснение:
4) Искомая площадь S=F(3)-F(0), где F(x)=∫(x²+1)*dx - первообразная функции y(x). Отсюда F(x)=1/3*x³+x+C, и тогда S=1/3*3³+3+C-C=12.
5) Разделив обе части уравнения на y, получаем уравнение с разделёнными переменными x²*dx=y*dy. Интегрируя, получаем: 1/2*y²=1/3*x³+C. Используя условие y(0)=1, приходим к уравнению 1/2=0+C, откуда C=1/2. Отсюда 1/2*y²=1/3*x³+1/2, или 3*y²-2*x³-3=0. Проверка: исходное уравнение можно записать в виде dy/dx=x²/y. Дифференцируя полученное решение по x, получаем: 6*y*y'-6*x²=0, откуда y'=dy/dx=x²/y, что совпадает с исходным уравнением - значит, уравнение решено правильно.
Угол между прямой AA1 и плоскостью ABC1 равен
arcsin(√6/3). Угол ≈ 54,7°
Пошаговое объяснение:
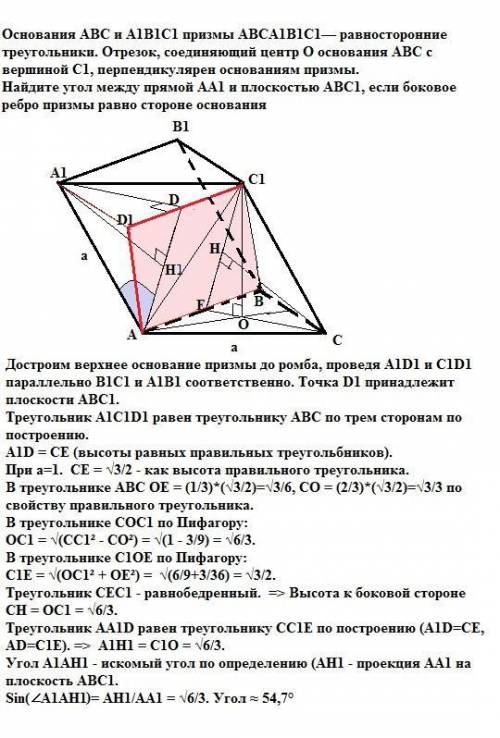
Достроим верхнее основание призмы до ромба, проведя A1D1 и C1D1 параллельно B1C1 и A1B1 соответственно. Точка D1 принадлежит плоскости АВС1.
Треугольник А1С1D1 равен треугольнику АВС по трем сторонам по построению.
A1D = CE (высоты равных правильных треугольбников).
При а=1. CE = √3/2 - как высота правильного треугольника.
В треугольнике АВС ОЕ = (1/3)*(√3/2)=√3/6, СО = (2/3)*(√3/2)=√3/3 по свойству правильного треугольника.
В треугольнике СОС1 по Пифагору:
ОС1 = √(СС1² - СО²) = √(1 - 3/9) = √6/3.
В треугольнике С1ОЕ по Пифагору:
С1Е = √(ОС1² + ОЕ²) = √(6/9+3/36) = √3/2.
Треугольник CEC1 - равнобедренный. => Высота к боковой стороне СН = ОС1 = √6/3.
Треугольник АА1D равен треугольнику СС1Е по построению (A1D=CE, AD=C1E). => A1H1 = C1O = √6/3.
Угол A1АН1 - искомый угол по определению (AH1 - проекция АА1 на плоскость АВС1.
Sin(∠A1AH1 = AH1/AA1 = √6/3. Угол ≈ 54,7°
Решение. Найдем точки разрыва функции внутри указанной области.
Находим переделы в точке x=1. В этой точке функция терпит разрыв. Предел равен ∞, поэтому это точка разрыва II-го рода.
Находим переделы в точке x=0 В этой точке функция терпит разрыв. Пределы существуют, но не равны, поэтому это точка разрыва I-го рода.
ответ: точка x1=1 является точкой разрыва II-го рода, точка x2=0 является точкой разрыва I-го рода.
В этой точке функция терпит разрыв. Предел равен ∞, поэтому это точка разрыва II-го рода.
Находим переделы в точке x=0
В этой точке функция терпит разрыв. Пределы существуют, но не равны, поэтому это точка разрыва I-го рода.
ответ: точка x1=1 является точкой разрыва II-го рода, точка x2=0 является точкой разрыва I-го рода.