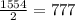1925
3773
9317
Пошаговое объяснение:
Приймем за х - наименьший делитель, а за у - наибольший делитель.
Тогда у : х = 77, а искомое число равно х*у или 77х².
По условию задачи есть ограничение:
10000 > 77x² > 999 (где 10000 - минимальное пятизначное число, а 999 - максимальное трёхзначное)
Упростим выражение:
11,4 > x > 3,6 ,
но так как х - целое, то более корректно неравенство будет выглядеть так: 11 ≥ х ≥ 4.
Этому условию отвечают целые числа: 4, 5, 6, 7, 8, 9, 10, 11.
Но в этом списке есть числа, у которых есть делитель, меньший заданного диапазона (2 или 3), поэтому из списка нужно выбрать только простые числа: 5, 7, 11.
Значит есть всего 3 возможных ответа, которые отвечают условию задачи.
Найдем их:
5²*77=1925,
7²*77=3773,
11²*77=9317.
Пошаговое объяснение:
Чтобы найти точки пересечения, приравняем эти функции.
Надо бы найти область определения, числа под корнями должны быть неотрицательные числа, но это сложно.
Проще будет проверить найденные корни.
Возведем в квадрат обе части
Тангенсы можно вычесть, но они влияют на область определения:
pi*x/4 ≠ pi/2 + pi*k
x ≠ 2 + 4k = 2*(2k + 1)
x не равно числам, которые делятся на 2, но не делятся на 4.
Кроме того, x ≠ 3; x ≠ 8/3
Вычитаем тангенсы, остаются дроби.
(x+1)/(x-3) = (x+4)/(3x-8)
(x+1)/(x-3) - (x+4)/(3x-8) = 0
(x+1)(3x-8) - (x+4)(x-3) = 0
3x^2 - 5x - 8 - x^2 - x + 12 = 0
2x^2 - 6x + 4 = 0
x^2 - 3x + 2 = (x - 1)(x - 2) = 0
x1 = 1; x2 = 2 - не подходит.
Проверяем x = 1
Оба корня определены и равны друг другу.
ответ: 1
2)
Возводим в квадрат обе части
Приводим к общему знаменателю
Знаменатели одинаковые, избавляемся от них
x^2 + x^2 - 2x + 1 + 2x^2 - 2x = 9
4x^2 - 4x - 8 = 0
x^2 - x - 2 = 0
(x + 1)(x - 2) = 0
x1 = -1; x2 = 2
Подробнее - на -
777 литра
Пошаговое объяснение:
Пусть в 1-сосуде Х литр воды, а во 2-сосуде 0 литр воды.
1-переливание. Переливаем с 1-сосуда во 2-сосуд:
1-сосуд: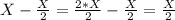
2-сосуд: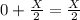
Объем воды в обоих сосудах в сумме дают Х литр!
2-переливание. Переливаем со 2-сосуда в 1-сосуд:
1-сосуд: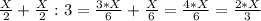
2-сосуд: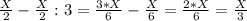
Объем воды в обоих сосудах в сумме дают Х литр!
3-переливание. Переливаем с 1-сосуда во 2-сосуд:
1-сосуд: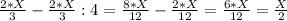
Так как, объем воды в обоих сосудах в сумме дают Х литр, то
2-сосуд:
Теперь покажем, что в нечётных числах переливания всегда
1-сосуд:
2-сосуд:
Пусть n=2·k+1.
n-переливание. Переливаем с 1-сосуда во 2-сосуд:
1-сосуд:
2-сосуд:
(n+1)-переливание. Переливаем со 2-сосуда в 1-сосуд:
1-сосуд: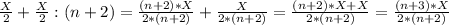
2-сосуд: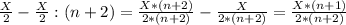
(n+2)-переливание. Переливаем с 1-сосуда во 2-сосуд:
1-сосуд: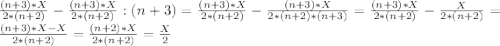
Так как, объем воды в обоих сосудах в сумме дают Х литр, то
2-сосуд:
что требовалось показать.
Отсюда, 2019 - нечётное и X=1554 литра, тогда
1-сосуд: