На столе лежит 101 кучка по 101 спичке. за один ход берется одна спичка из любой кучки. двое игроков ходят по очереди. если не позднее 1-го хода бу-дет взята последняя спичка из какой-то кучки, взявший её выигрывает, иначе — ничья. может ли кто-то из игроков выиграть независимо от игры соперника, и если да, то кто?
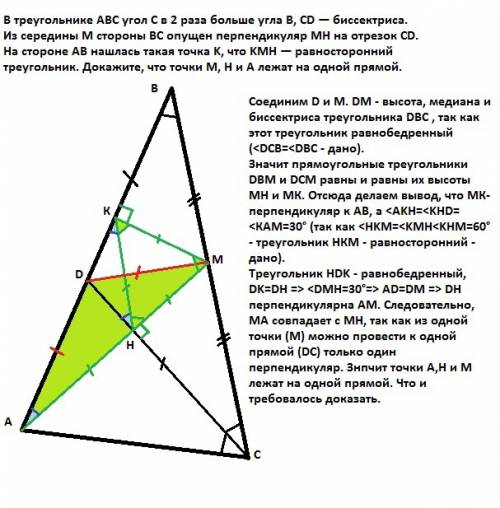
Соединим D и М. DM - высота, медиана и биссектриса треугольника DBC , так как этот треугольник равнобедренный (<DCB=<DBC - дано).
Значит прямоугольные треугольники DBM и DCM равны и равны их высоты МН и МК. Отсюда делаем вывод, что МК-перпендикуляр к АВ, а <AKH=<KHD=<КАМ=30° (так как <HKM=<KMН<KHM=60° - треугольник НКМ - равносторонний - дано).
Треугольник HDK - равнобедренный, DK=DH => <DMH=30°=> AD=DM => DH перпендикулярна АМ. Следовательно, МА совпадает с МН, так как из одной точки (М) можно провести к одной прямой (DC) только один перпендикуляр. Значит точки А,Н и М лежат на одной прямой.
Что и требовалось доказать.