найти объем пирамиды, полученной пересечением данной плоскости и координатных плоскостей xoy,xoz,yoz
x+4y+13z-23=0

👇

Увидеть ответ

Ответ:

VIRUS00000

10.10.2022

Дана плоскость x+4y+13z-23=0.

Преобразуем её уравнение "в отрезках".

Для этого свободный член перенесём вправо и разделим обе части уравнения на это число.

(x/23) + (y/(23/4)) + (z/(23/13) = 1.

Площадь основания So = (1/2)*23*(23/4) = (529/8) кв.ед.

Высоту нашли как координату z: Н = 23/13.

Тогда V = (1/3)SoH = (1/3)*(529/8)*(23/13) = (12167/312) ≈ 39,0 куб.ед..

4,8(60 оценок)

Открыть все ответы

Ответ:

darinakor140197nooii

10.10.2022

Разница в стоимости 1 кг сахара составляет 6 рублей, следовательно, минимальное количество сахара, за которым имеет смысл ехать в магазин "Дальний", должно быть не менее 9 кг: 6 (руб) х 9 (упаковок сахара) = 54. В таком случае стоимость покупки, включая проезд, обойдется нам в 320 рублей ((9 х 30) + 50), в то время как в магазине "Первый" мы бы потратили 324 рубля. Какая-никакая, а выгода!

Ехать за меньшим количеством сахара, например, за 8-ью кг будет невыгодно, так как 6 х 8 = 48 р. В таком случае покупка в "Дальнем" обошлась бы нам в 290 руб. ((30 х 8) + 50), а в "Ближнем" - 288 руб.

ответ: 9 кг.

4,8(48 оценок)

Ответ:

LoveSmile78900987

10.10.2022

Можно найти несколько пределов данной числовой последовательности. Для этого нужно посмотреть, что произойдет с ней при стремлении к бесконечности с разными знаками, и в "опасных" точках.

"Опасные" точки сразу видны, это:
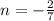1) $n=- \frac{2}{7}$ - знаменатель обращается в 0.
2) n=0

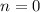- по обычаю проверяется эта точка.

Эта числовая последовательность может быть сведена ко второму замечательному пределу для нахождения пределов:
$lim (1+ \frac{1}{x})^x=e$ (при

→∞)

Выделяем целую часть в дроби:

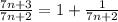
$\frac{7n+3}{7n+2 } = 1 + \frac{1}{7n+2 }$

Используем свойство 2-го замечательного предела, но добавляем степени:

$lim (1 + \frac{1}{7n+2 })^{3n-4}$

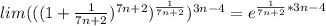$lim (((1 + \frac{1}{7n+2 })^{7n+2})^{ \frac{1}{7n+2}})^{3n-4} = e^{\frac{1}{7n+2} * 3n-4}$ (при

→∞)

То есть мы степень не меняли: домножили и разделили.

Посчитаем, что получилось:

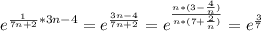$e^{\frac{1}{7n+2} * 3n-4} = e^{ \frac{3n-4}{7n+2}} = e^{ \frac{n*(3-\frac{4}{n}) }{n*(7+\frac{2}{n})} } = e^{ \frac{3}{7} }$ (при

→∞)

Итак:
1)

→+∞ предел равен $e^{ \frac{3}{7} }$
2)

→-∞ предел равен $e^{ \frac{3}{7} }$

3)

→0 предел равен:
$lim ( \frac{7n+3}{7n+2})^{3n-4} = (\frac{3}{2})^{-4} = (\frac{2}{3})^{4} = \frac{16}{81}$

4)

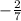
→ $- \frac{2}{7}$
По правило Лопиталя имеем: 0 (не расписывал, поскольку это очень много и неважно в данном случае, нас это не интересует).

Мы видим, что при стремлении к бесконечности с разными знаками, мы имеем конечное число. В "опасных" точках, скачков нет.

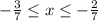Используя свойства показательной функции, находим, что график делает скачок в некотором интервале (основание должно быть неотрицательным числом, если же взять число из интервала $- \frac{3}{7} \leq x \leq - \frac{2}{7}$ - мы получаем отрицательное основание).

Можно говорить, что данная числовая последовательность является неограниченной (из-за этого интервала).

Если же этого не учитывать, то данная числовая последовательность является ограниченной (это очень грубо).

Найдите предел числовой последовательности. укажите, является ли заданная числовая последовательност