171 (единиц²).
Пошаговое объяснение:
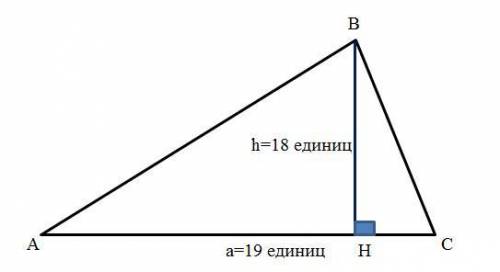
Дано :
ΔАВС (см. рисунок) :
a = AC = 19 единиц;
h = BH ⊥ AC, т.е. h - высота, опущенная на сторону a = AC.
BH = 18
Найти: S(ΔABC).
Применим стандартную теорему о площади треугольника:
Площадь треугольника равна половине произведения его стороны и высоты, опущенной на эту сторону.
Следовательно, по нашим обозначениям:
S(ΔABC) = 0,5·AC·BH или S(ΔABC) = 0,5·a·h.
Тогда
S(ΔABC) = 0,5·19·18 = 19·9 = 171 (единиц²).
70 кг
Пошаговое объяснение:
m₁ - масса 6%-го раствора кислоты, кг.
m₂ - масса 74%-го раствора кислоты, кг.
Система уравнений:
0,06m₁+0,74m₂=0,19(m₁+m₂+10)
0,06m₁+0,74m₂+0,5·10=0,24(m₁+m₂+10)
0,06m₁+0,74m₂=0,19m₁+0,19m₂+1,9
0,06m₁+0,74m₂+5=0,24m₁+0,24m₂+2,4
0,06m₁+0,74m₂-0,19m₁-0,19m₂=1,9
0,06m₁+0,74m₂-0,24m₁-0,24m₂=2,4-5
0,55m₂-0,13m₁=1,9 |×100
0,5m₂-0,18m₁=-2,6 |×100/2
55m₂-13m₁=190
9m₁-25m₂=130
55m₂-13m₁+9m₁-25m₂=190+130
30m₂-4m₁=320 |2
15m₂-2m₁=160; 2m₁=15m₂-160; m₁=(15m₂-160)/2
9(15m₂-160)/2 -(50m₂)/2=130
135m₂-1440-50m₂=260
85m₂=260+1440
m₂=20 кг - масса 74%-го раствора кислоты.
15·20-2m₁=160
m₁=(300-160)/2=140/2=70 кг - масса 74%-го раствора кислоты.
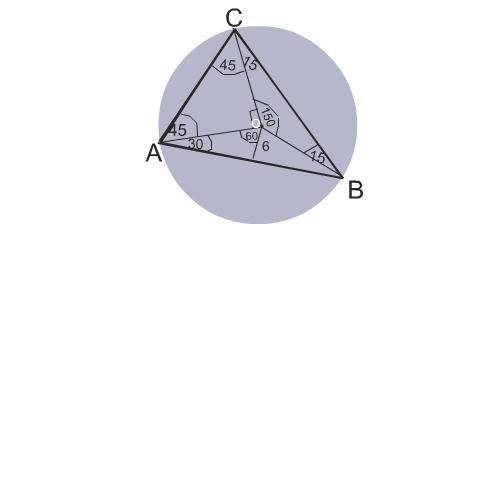
Радиусами окружности исходный треугольник АВС делится на 3 равнобедренных треугольника.
В трегольнике СОВ острые углы равны по 15 градусов, поэтому
угол СОВ равен 180-30=150 градусов.
Угол СОА равен 90 градусов по условию задачи.
Отсюда
угол АОВ равен 360 -90-150=120 градусов.
Расстояние от О до АВ равно 6 см.
Этот отрезок делит треугольник АОВ на два прямоугольных треугольника,острый угол ОАВ равен 30 градусов.
Радиус ОА в этом треугольнике является гипотенузой и вдвое больше катета, противолежащего углу 30 градусов.
Радиус окружности равен
6*2=12 см
Дано :
ΔАВС.
АС = 19.
ВН - высота.
ВН = 18.
Найти :
S(ΔABC) = ?
Площадь треугольника равна половине произведения его стороны и высоты, опущенной на эту сторону.Следовательно -
S(ΔABC) = 0,5*ВН*АС
S(ΔABC) = 0,5*18*19
S(ΔABC) = 0,5*342
S(ΔABC) = 171 (ед²).
171 (ед²).