30 домов
170 саженцев
Пошаговое объяснение:
9x=y+1005x=y-20x=(y-20)/5x=0.2y-49*(0.2y-4)=y+1001.8y-36=y+1001.8y-y=100+360.8y=136y=136/0.8y=170x=0.2*170-4x=30
(см. объяснение)
Пошаговое объяснение:
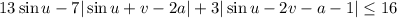
Введем замену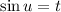 
. Откуда 
.
Тогда неравенство примет вид:
Пусть переменная здесь будет 
, а 
и 
параметры.
Наша задача определить, когда в решении этого неравенства будет содержаться промежуток ![[-1;\;1]](/tpl/images/2011/3499/001ed.png)
.
Заметим, что при любом раскрытии модулей перед буквой будет стоять положительное число.
Тогда при любых значениях параметров имеем возрастающую функцию 
.
Значит промежуток будет в решении неравенства, если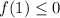 
, откуда переходим к новой записи:
Тогда пришли к неравенству:
Строим его в координатах 
и выделяем интересующую нас область:
(см. прикрепленный файл)
Итого при ![a\in\left[\dfrac{1}{5};\;\dfrac{3}{5}\right]](/tpl/images/2011/3499/9a62e.png)
исходное неравенство выполнимо для любой пары 
действительных чисел 
.
Задание выполнено!
Если речь идёт о кратности чисел, то рассматривается целые числа. Поэтому определим целые решения неравенств. Z - множество целых чисел.
1) 120 < х < 170
x∈[121; 169], x∈Z
Наименьшее число из [121; 169], которое кратно 9, это 126 (по признаку делимости: сумма цифр 9 делится на 9). Каждое следующее кратное число больше предыдущего кратного числа на 9:
126; 135; 144; 153; 162
2) 81 < y ≤ 99
x∈[82; 99], x∈Z
Наибольшее число из [82; 99], которое кратно 9, это 99 (по признаку делимости: сумма цифр 18 делится на 9). Каждое предыдущее кратное число меньше от следующего кратного числа на 9:
90; 99
3) 63 ≤ z ≤ 117
x∈[63; 117], x∈Z
Наименьшее число из [63; 117], которое кратно 9, это 63 (по признаку делимости: сумма цифр 9 делится на 9). Каждое следующее кратное число больше предыдущего кратного числа на 9:
63; 72; 81; 90; 99; 108; 117
Пусть, количество домов х, тогда количество саженцев 9х - 100 или 5х + 20. Составляем и решаем уравнение:
9х-100=5х+20
9х-5х=20+100
4х=120
х=30
30 домов
5*30+20=170 саженцев
ответ: 170 саженцев и 30 домов.