3/7 + 5/8 : 7/40 = 3/7 + 5/8 * 40/7 = 3/7 + 5/1 * 5/7 = 3/7 + 25/7 = 28/7 = 4
Пошаговое объяснение:
3/7+5/8:7/40
1. 3/7 , 5/8 и 7/40 - это обычные дроби.
2. Проводим решение по правилам очередности выполнения действий, в нашем случае сначала деление, потом сложение.
3. Выполняем деление 5/8 : 7/40 по правилу деления обычных дробей, а именно, при делении двух обычных дробей, действие проводится через умножение этих дробей, при этом дробь делитель (7/40) записывается обратной , т.е. 40/7.
5/8 : 7/40 = 5/8 * 40/7
При действии умножение двух обычных дробей, можем провести сокращение этих дробей: 8 и 40 есть кратное 8, т.е. 8 и 40 делим на 8. В знаменателе дроби 5/8 остается 1, а в числителе дроби 40/7 - остается 5.
Записываем результат сокращения дробей: 5/8 = 5/1, а 40/7 = 5/7, т.е. 5/1 * 5/7 и проводим действие умножения по правилам умножения простых дробей, т.е. числитель первой дроби множим на числитель второй дроби, произведение записываем в числитель, и аналогично знаменатель, и произведение записываем в знаменатель.
5/1 * 5/7 = (5 * 5) / (1 * 7) = 25/7
4. Далее переходим к действию сложения двух дробей: 3/7 + 25/7.
У нас дроби с одинаковыми знаменателями, значит можем сложить по правилу сложения двух дробей с одинаковыми знаменателями, а именно числитель первой дроби необходимо сложить с числителем второй дроби, сумму записать в числитель, а знаменатель записываем без изменения, т.е. 3/7 + 25/7 = (3+25) / 7 = 28 / 7
5. У нас вышел результат: 28/4, а значение дроби равно частному от деления числителя дроби на знаменатель дроби, т.е. дробь 28/74 = 28 : 7 = 4. ответ решения: 4
3/7 + 5/8 : 7/40 = 3/7 + 5/8 * 40/7 = 3/7 + 5/1 * 5/7 = 3/7 + 25/7 = 28/7 = 4
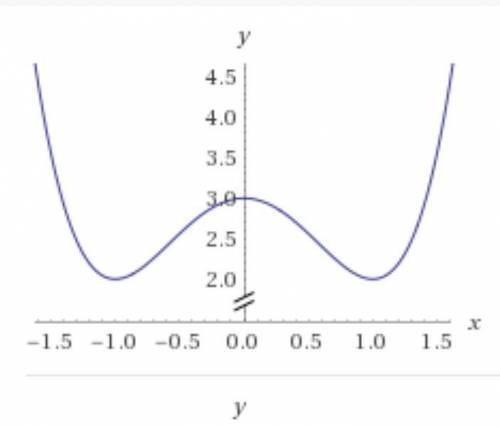
Дана функция f(x)=x^4 - 2x² + 3.
Её производная равна f(x) = 4x^3 - 4x = 4x(x² - 1).
Приравняв производную нулю, получаем 3 критические точки: х = 0 и х = +-1.
Находим знаки производной на промежутках (-∞; -1), (-1; 0), (0; 1), (1; ∞).
x = -2 -1 -0,5 0 0,5 1 2
y' = -24 0 1,5 0 -1,5 0 24 .
В точках х = +-1 есть 2 общих минимума, у(мин) = 2,
в точке х = 0 местный максимум.
Так как функция чётная, то на заданном промежутке максимальное значение функции в точке х = -4.
у = (-4)^4 - 2*(-4)² + 3 = 227.
Подставляем в уравнение окружности.
Упрощаем уравнение и решаем его относительно у. Так как у нас окружность и прямая имеют всего одну точку => дискриминант равен 0.