Номер 1: ОДЗ - Область допустимых значений. Такие значения икс, при которых существуют левая и правая части неравенства
Под буквой А нам подходят все иксы, так как нет никаких ограничений
Под буквой Б наше ОДЗ примет вид (для первой дроби) x∈(-∞;-3)∪(-3;+∞), а для второй дроби ОДЗ x∈(-∞;3)∪(3;+∞), так как при x = ±3 у нас в знаменателях оказываются нули, чего быть недолжно
Под буквой В упростим знаменатель второй дроби, вынеся общий множитель. И будет тогда x(x+2). ОДЗ первой дроби x∈(-∞;-2)∪(-2;+∞), а второй дроби x∈(-∞;-2)∪(-2;0)∪(0;+∞), так как при x = -2 и x = 0 у нас нули в знаменателях
Номер 2: Запишем суммы:
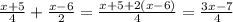
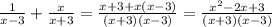
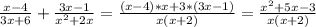
Номер 3: ОДЗ несократимых дробей: 1-ая дробь - все числа. 2-ая - все числа, кроме x = ±3. 3-я - все числа, кроме x=0 и x= -2
Номер 4:
Найдем значение дроби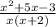 
при x = -1. Тогда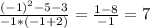 
При х = 0.25 у нас будет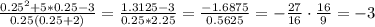 
При х = 2 у нас будет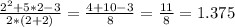 
Пошаговое объяснение:
Переведем градусы в радианы:
α[рад] = a[°] * π/180°,
где a[°] — градусная мера угла, α[рад] — радианная мера угла.
а) Найдем радианную меру угла, равного 25°:
α[рад] = 25° * π/180° = (25° * π)/180° = 5π/36
в)α[рад] = 36° * π/180° = (36° * π)/180° = π/5
д)α[рад] = 135° * π/180° = (135° * π)/180° = 3π/4
ж)α[рад] = 810° * π/180° = (810° * π)/180° = 9π/2
б)α[рад] = 573° * π/180° = (573° * π)/180° = 191π/60
г)α[рад] = 20° * π/180° = (20° * π)/180° = π/9
е) α[рад] = -150° * π/180° = (-150° * π)/180° = -5π/6
з)α[рад] = 2160° * π/180° = (2160° * π)/180° = 12π
36 см³
Пошаговое объяснение:
V= Sосн.*H - объём призмы
Sосн = SΔ - площадь прямоугольного треугольника
H = 6 см - высота призмы
a=3 см - катет, с= 5 см - гипотенуза
b = √(c²-a²) = √(5²-3²) = √(25-9) = √16 = 4 (см) - катет
SΔ = ab/2 = 3*4/2 = 6 (см²)
Sосн = 6 см²
V = Sосн.*H
V = 6 * 6 = 36 (см³) - объём призмы