Три числа относятся как 2,5,7 причом сумма наибольшего и наименьшего числа равна 63 найдите сумму этих трёх чисел

👇

Увидеть ответ

Ответ:

DashaLatysheva1

24.12.2020

ответ: 2*х+7*х=9*х=63 или х=63/9=7. Искомая сумма равна 7*(2+5+7)=7*14=98.

ответ 98.

Пошаговое объяснение:

4,7(33 оценок)

Открыть все ответы

Ответ:

olga000064

24.12.2020

1) Найти области определения и значений данной функции f.

Для аргумента и функции нет ограничений: их значения - вся числовая ось.

2) Выяснить, обладает ли функция особенностями, облегчающими исследование, т. е. является ли функция f: а) четной или нечетной:

f(-x)=(-x)³−1 = -x³−1 = -(x³+1). Значит, функция не чётная и не нечётная.

б) не периодическая.

3) Вычислить координаты точек пересечения графика с осями координат:

- пересечение с осью Оу (х = 0), у = -1.

- пересечение с осью Ох (у = 0), x³−1 = 0, x³ = 1, x = ∛1 = 1.

4) Найти промежутки знакопостоянства функции f.

На основе нулей функции имеем:

- функция отрицательна при х < 1 (x ∈ (-∞; 1),

- функция положительна при х > 1 (x ∈ (1; +∞).

5) на каких промежутках функция f возрастает, а на каких убывает.

Найти точки экстремума, вид экстремума (максимум или минимум) и вычислить значения f в этих точка.

Находим производную функции и приравниваем нулю.

y' = 3x² = 0, x = 0 это критическая точка. Находим знаки производной левее и правее этой точки. Так как переменная в квадрате, то знак её положителен. Значит, функция на всей области определения возрастает.

Поэтому не имеет ни минимума, ни максимума.

6) Вторая производная y'' = 6x. Поэтому в точке х = 0 функция имеет перегиб. При x < 0 график функции выпуклый, при x > 0 вогнутый.

7) Асимптот функция не имеет.

Решить . : исследование функций проведите по общей схеме исследование функции и постройте ее график.

4,8(50 оценок)

Ответ:

sdfsdfsddf

24.12.2020

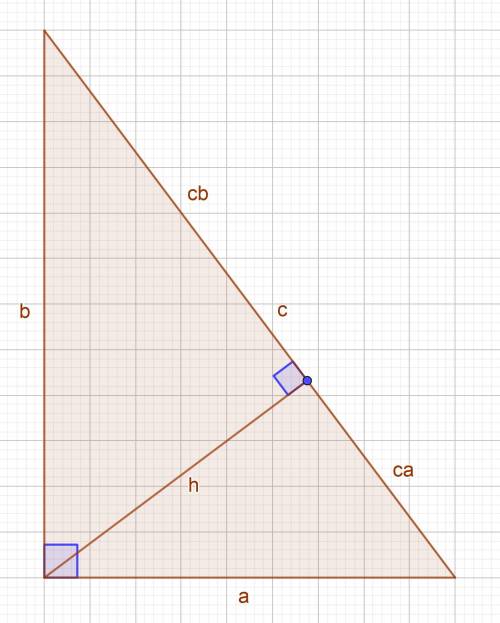
Обозначим катеты за a = 9 см, b = 12 см , гипотенузу за c, высоту за h, проекции катетов на гипотенузу за ca и ba.

Исходя из т. Пифагора, следует:

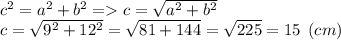
$c^2=a^2+b^2 = c=\sqrt{a^2+b^2} \\c = \sqrt{9^2+12^2}= \sqrt{81+144} = \sqrt{225} = 15 \:\: (cm)$

Найдет площадь прямоугольного треугольника:

$S = \frac{a\cdot b}{2} \\S = \frac{9\cdot 12}{2} = 9\cdot 6 = 54 \:\: (cm^2)$

Воспользуемся формулой площади треугольника через высоту и выразим из нее высоту:

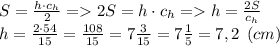
$S = \frac{h\cdot c_h}{2} = 2S = h\cdot c_h = h = \frac{2S}{c_h} \\h = \frac{2\cdot 54}{15} = \frac{108}{15}= 7\frac{3}{15} =7\frac{1}{5}=7,2 \:\: (cm)$

Проекции катетов будут равны:

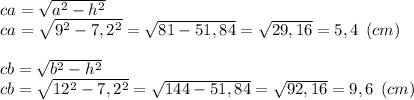
$ca = \sqrt{a^2-h^2} \\ca = \sqrt{9^2-7,2^2} = \sqrt{81-51,84}= \sqrt{29,16} = 5,4 \:\: (cm) \\\\cb = \sqrt{b^2-h^2} \\cb = \sqrt{12^2-7,2^2} = \sqrt{144-51,84}= \sqrt{92,16} = 9,6 \:\: (cm)$

или 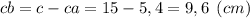$cb = c-ca = 15-5,4 = 9,6 \:\: (cm)$

—————————————————————————————

Высоту и проекции катетов также можно найти через пропорциональные отрезки в прямоугольном треугольнике:

– высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу:

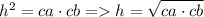
$h^2 = ca\cdot cb = h=\sqrt{ca\cdot cb}$

– катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу:

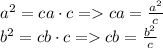
$a^2 = ca\cdot c = ca = \frac{a^2}{c} \\b^2 = cb\cdot c = cb = \frac{b^2}{c}\\\\$

—————————————————————————————

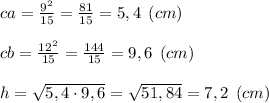
$ca=\frac{9^2}{15} = \frac{81}{15} = 5,4 \:\: (cm) \\\\cb=\frac{12^2}{15} = \frac{144}{15} = 9,6 \:\: (cm) \\\\h=\sqrt{5,4\cdot 9,6} =\sqrt{51,84} = 7,2 \:\: (cm)$