Для перевезення вантажу використовують машини типів а та б. вантажопід'ємніть машин кожного типу - 3т. за один рейс машина а витрачає 1,5кг мастильних матеріалів і 50л бензину, а машина б - відповідно 2кг і 30л. на базі є 35кг мастильних матеріалів і 900л бензину. витрати на експлуатацію машини а становлять 6 у.г.о., б- 5 у.г.о. треба перевезти 60т вантажу. скільки потрібно використати машин типів а і б, щоб експлуатаційні витрати були мінімальними?
у.г.о- умовно грошова одиниця

👇

Открыть все ответы

Ответ:

evakuleva

11.02.2023

Сейчас 20.12.2012 г . 9 ч. 27 мин. утра

1) ответ: 20.12.2012 г. 18 ч. 02 мин.
9 ч. 27 мин. + 8 ч. 35 мин.= 17 ч. + 62 мин. = 18 ч. 02 мин.
или 6 ч. 02 мин. (вечера)

2) ответ: 21.12.2012 19 ч. 40 мин.
34 ч. 13 мин. = 1 сутки 10 ч. 13 мин.
20.12.12 9 ч. 27 мин. - 21.12. 9 ч. 27 мин. - 1 сутки
9 ч. 27 мин. + 10 ч. 13 мин. = 19 ч. 40 мин.

3) ответ: 31.12.12 12 час. 00 мин.
20.12.12 9ч. 27 мин. + 11 суток = 31.12.12 9 ч. 27 мин. (утра)
31.12.12 9 ч. 27 мин. + 2 ч. 33 мин.= 31.12.12 12 часов 00 мин. (дня)

4,7(51 оценок)

Ответ:

Василий2005

11.02.2023

точка A(1;-2) расположена вне окружности

Пошаговое объяснение:

Решим задание через определение степени точки относительно окружности

Степенью точки относительно данной окружности называется разность

${ d^{2}-R^{2}} ,$

d — расстояние от точки до центра окружности,

R — радиус окружности.

Точки имеют следуюющие степени в зависимости от расположения:

- вне окружности - положительную,

- внутри окружности - отрицательную,

- на окружности - нулевую.

Общее уравнение окружности задается уравнением

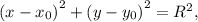
$\left(x-x_{0}\right)^{2}+\left(y-y_{0}\right)^{2}=R^{2},$

где (х0, у0) - координаты центра окружности

R - ее радиус.

В нашем случае:

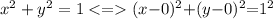
$x^2+y^2 = 1 < = (x{ - }0) {}^{2}{ +} (y{ -} 0) {}^{2}{ = } {1}^{2}$

Следовательно,

радиус окружности R = 1;

центр окружности O = О(0; 0)

Теперь вычислим степень точки A(1;-2) относительно этой окружности:

$A = A(1;-2); \: \: \: O =O(0;0); \: \: { R = 1} , \\ d=|AO|=\sqrt{(A_x-O_x)^2+(A_y-O_y)^2} \\ d = \sqrt{(1 - 0) {}^{2} + ( - 2 - 0) {}^{2} } = \\ = \sqrt{ {1}^{2} + ( - 2) {}^{2} \: } = \sqrt{1 + 4} = \sqrt{5} \\ {d}^{2} - {R}^{2} = ( \sqrt{5} )^{2} - {1}^{2} = 5 - 1 = 4 0$