Задание 1
Пусть х - работает первый насос, у - работает второй насос (производительность в минуту) , а Р - вся работа.
Р/(х+у)=20мин
Р/х=30
Из Р/х=30 найдем Х
х=Р/30
Подставим в первое уравнение:
Р/(Р/30+у)=20
Р=20*(Р/30+у)
Р=2/3Р+20у
20у=Р/3
у=Р/60 - это означает что производительность насоса равна вся работа деленная на 60 минут, то есть потребуется 60 мин , чтобы второй насос перекачал нефть
ответ. 60 минут
Задание 2
( 7,85х - 12,4х ) * (-1 9/91) = - 2 11/12 - 1 2/3
-4.55х* (- 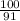 ) =
) = 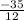 -
- 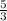
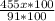 =
= 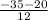
5x= 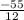
x= 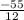 *
* 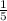
x= 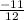
Задание 1
Пусть х - работает первый насос, у - работает второй насос (производительность в минуту) , а Р - вся работа.
Р/(х+у)=20мин
Р/х=30
Из Р/х=30 найдем Х
х=Р/30
Подставим в первое уравнение:
Р/(Р/30+у)=20
Р=20*(Р/30+у)
Р=2/3Р+20у
20у=Р/3
у=Р/60 - это означает что производительность насоса равна вся работа деленная на 60 минут, то есть потребуется 60 мин , чтобы второй насос перекачал нефть
ответ. 60 минут
Задание 2
( 7,85х - 12,4х ) * (-1 9/91) = - 2 11/12 - 1 2/3
-4.55х* (- 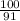 ) =
) = 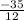 -
- 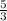
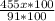 =
= 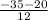
5x= 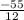
x= 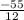 *
* 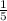
x= 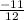
120
Пошаговое объяснение:
Задача вероятнее всего на русском языке звучит так:
Сторона правильного вписанного многоугольника видна из центра окружности под углом 3°. Сколько сторон (углов) у многоугольника?
Сумма всех центральных углов многоугольника равна 360°, а угол, под которым видна сторона правильного вписанного многоугольника - это как раз центральный угол α. В нашем случае α=3°.
Количество сторон (углов) правильного многоугольника вычисляют по формуле: n= 360°/α.
Итак, n=360°/3°=120 -это и есть количество сторон (углов) правильного многоугольника.