Вычислите:
а) 2 - 39,
г) 4 - 2 - 32 + (-1);
ж) 4.0 + (-2)+5';
са
б) (-2)— 2°;
д) 2. (-3)2 + 9 — 4°;
3) (-3)= -2 -2- (-3)";
в) (-2) – (-2) – (-2):
е) (-1) - (-8) + 4 — 2°;
и) (-80 + 85)* + (4 – 7).

👇

Увидеть ответ

Открыть все ответы

Ответ:

Marketing23

22.02.2023

$x^{2} + y^{2} = 8$ — уравнение окружности с центром $(0; \ 0)$ и радиусом $\sqrt{8}.$

$y^{2} = 2x$ — уравнение параболы

Изобразим графики данных уравнений и найдем площадь образовавшейся фигуры в правой полуплоскости.

Выразим ординаты данных уравнений:

$y = \pm\sqrt{8 - x^{2}}$ и $y = \pm\sqrt{2x}$

Так как имеем симметричные фигуры, найдем площадь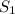 $S_{1}$ одной из них. Общая их площадь 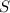будет состоять из площади двух 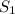$S_{1}$ , то есть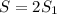 $S = 2S_{1}$

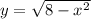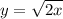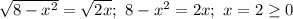
Тогда $y =\sqrt{8 - x^{2}}$ и $y = \sqrt{2x}$ . Поэтому $\sqrt{8 - x^{2}} = \sqrt{2x}; \ 8 - x^{2} = 2x; \ x = 2 \geq 0$

Так как окружность вытесняет больше площади, чем парабола, то имеем разность их площадей, определяющаяся через определенный интеграл:

$S_{1} = \displaystyle \int\limits^{2}_{0} {\left(\sqrt{8 - x^{2}} - \sqrt{2x} \right)} \, dx = \int\limits^{2}_{0} {\sqrt{8 - x^{2}}} \, dx - \int\limits^{2}_{0} { \sqrt{2x} } \, dx$

Найдем первый интеграл геометрически: площадь круга находится по формуле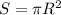 $S = \pi R^{2}$ , где 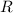— радиус круга. Тогда четверть круга: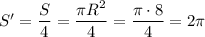 $S' = \dfrac{S}{4} = \dfrac{\pi R^{2}}{4} = \dfrac{\pi \cdot 8}{4} = 2\pi$

Найдем второй интеграл по формуле Ньютона-Лейбница:

$\displaystyle \int\limits^{2}_{0} { \sqrt{2x} } \, dx = \dfrac{2\sqrt{2x^{3}}}{3} \bigg|_{0}^{2} = \dfrac{2\sqrt{2 \cdot 2^{3}}}{3} - \dfrac{2\sqrt{2 \cdot 0^{3}}}{3} = \dfrac{8}{3}$

Таким образом,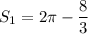 $S_{1} = 2\pi - \dfrac{8}{3}$ кв. ед.

Тогда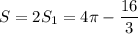 $S = 2S_{1} = 4\pi - \dfrac{16}{3}$ кв. ед.

ответ: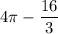 $4\pi - \dfrac{16}{3}$ кв. ед.

Найти площадь фигуры, лежащей в правой полуплоскости и ограниченной окружностью x^2+y^2=8 и параболо

4,8(43 оценок)

Ответ:

AvdAda24

22.02.2023

По теореме о внешнем угле треугольника получим, что сумма двух углов треугольника, не смежных с внешним, будет равна 90 градусам, тогда по теореме о сумме углов треугольника третий внутренний угол будет равен 180 - 90 = 90 градусов, т.е. угол, смежный с внешним, будет прямой. Предположим, что второй внешний угол при другой вершине также прямой. Аналогично, смежный с внешним угол треугольника будет равен 90 градусам (прямой). Но треугольника с двумя прямыми углами не существует, следовательно утверждение неверно.

4,6(29 оценок)

Это интересно:

Компьютеры-и-электроника

08.01.2022

Как превратить видео в живые обои на Android...

Образование-и-коммуникации

26.09.2021

Как понимать людей: психологические аспекты взаимодействия...

Компьютеры-и-электроника

19.07.2021

Как контролировать контент на YouTube с помощью блокирования по ключевым словам?...

Мир-работы