 и
и 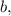 а уравнение всего одно:
а уравнение всего одно: 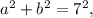 то решений может быть бесконечно много.
то решений может быть бесконечно много.
 а значит:
а значит: 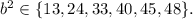
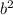 – не является квадратом натурального числа, а значит, целых решений нет.
– не является квадратом натурального числа, а значит, целых решений нет.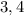 и
и  и рассчитать катеты из подобия гипотенузы
и рассчитать катеты из подобия гипотенузы  этого треугольника и нашего исходного треугольника с гипотенузой
этого треугольника и нашего исходного треугольника с гипотенузой  Ясно, что наш треугольник больше и относится к упомянутому египетскому, как
Ясно, что наш треугольник больше и относится к упомянутому египетскому, как  т.е. больше него в
т.е. больше него в 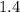 раза, соответственно и катеты больше в
раза, соответственно и катеты больше в 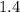 раза, т.е. вместо катетов
раза, т.е. вместо катетов 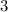 и
и 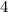 исходного египетского нужно брать катеты
исходного египетского нужно брать катеты 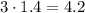 и
и 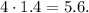
 и
и 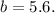
 ;
;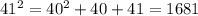 ;
;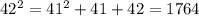 ;
; ;
; ;
;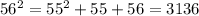 ;
; ;
;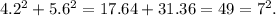
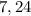 и
и  и рассчитать катеты из подобия гипотенузы
и рассчитать катеты из подобия гипотенузы  этого треугольника и нашего исходного треугольника с гипотенузой
этого треугольника и нашего исходного треугольника с гипотенузой  Ясно, что наш треугольник меньше и относится к упомянутому египетскому, как
Ясно, что наш треугольник меньше и относится к упомянутому египетскому, как 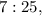 т.е. составляет от него часть:
т.е. составляет от него часть: 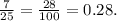 Соответственно и катеты меньше, т.е. вместо катетов
Соответственно и катеты меньше, т.е. вместо катетов  и
и 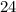 исходного египетского нужно брать катеты
исходного египетского нужно брать катеты 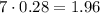 и
и 
 и
и 
 и
и 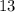 и рассчитать катеты из подобия гипотенузы
и рассчитать катеты из подобия гипотенузы 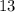 этого треугольника и нашего исходного треугольника с гипотенузой
этого треугольника и нашего исходного треугольника с гипотенузой  Ясно, что наш треугольник меньше и относится к упомянутому египетскому, как
Ясно, что наш треугольник меньше и относится к упомянутому египетскому, как  т.е. составляет от него часть:
т.е. составляет от него часть: 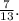 Соответственно и катеты меньше, т.е. вместо катетов
Соответственно и катеты меньше, т.е. вместо катетов  и
и 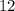 исходного египетского нужно брать катеты
исходного египетского нужно брать катеты  и
и 
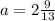 и
и 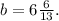
 и
и 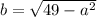
 и
и 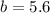 ;
; и
и 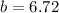 ;
;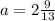 и
и 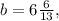 кроме которых существует бесконечное число аналогичных рациональных решений.
кроме которых существует бесконечное число аналогичных рациональных решений.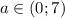 и
и 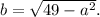
2
Пошаговое объяснение:
ctg(x)=cos x/ sin x
lim cos x* ln(x+exp(x))/ sin x = lim (cos x * ln(x+exp(x)))' / (sin x)' = lim((cos x)' * ln(x+exp(x)) + cos x * (ln(x+exp(x)))' )/cos x = lim (-sin x * ln(x+exp(x)) + cos x * (1+exp(x)/(x+exp(x/cos x = lim( -sin x * ln(x+exp(x))) / cos x + (1+exp(x))/(x+exp(x));
-sin x / cos x = 0 в пределе x->0 , следовательно первый множитель =0, во второй множитель подставляем х=0 и получаем ответ 2