ответ:
когда меньше нуля > 0
и когда - 1
Пошаговое объяснение:
Расстояние между пунктами 78 км.
Направление движения: на встречу друг другу.
Выехали из двух пунктов одновременно.
Скорость первого дилижанса 12 км/ч.
Скорость второго дилижанса 14 км/ч.
Определить через какое время встретятся дилижансы.
S = v * t, где s — пройденный путь (км), v — скорость движения (км/ч), t — время (ч), за которое пройден путь S.
Определим расстояние, которое проезжают оба дилижанса за час:
S = (12 + 14) * 1 = 26 км — расстояние, которое проезжают оба дилижанса за час.
Определим время через которое встретятся дилижансы:
78 : 26 = 3(ч)
ответ: дилижансы встретятся через 3 часа.
Пошаговое объяснение:
Чтобы перевести обыкновенную дробь в десятичную можно:
Разделить числитель на знаменатель (но это не всегда удобно, некоторые дроби кратные числам 10, 100, 1000 и т.п. можно перевести сразу)Если дробь кратна 10, 100, 1000 и т.п., можно умножить ее на такое число, чтобы получилось 10, 100, 1000 и т.п.Таким образом, дроб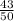и 
и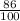 
можно преобразовать в десятичные.
Чтобы преобразовать 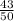в десятичную, нам надо ее умножить на такое число, чтобы произведение знаменателя и этого числа было кратно 10. То есть надо эту дробь умножить на 100 : 50 = 2 (и числитель, и знаменатель). Таким образом получаем 
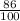= = 0,86
Дробь 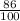уже имеет знаменатель кратный 10. Так что мы преобразуем ее в десятичную 0,86
возможность может нет иметь решений если
\frac{7}{a} = \frac{1}{b} = \frac{5}{6}
a
7
=
b
1
=
6
5
запишем в систему
\begin{lgathered}\left \{ {{ \frac{7}{a}= \frac{1}{b} } \atop { \frac{7}{a}= \frac{5}{6} }} \right. \to \left \{ {{a=7b} \atop {42=5\cdot 7b}} \right. \\ a=1.2 \\ b= \frac{6}{35}\end{lgathered}
{
a
7
=
6
5
a
7
=
b
1
→{
42=5⋅7b
a=7b
a=1.2
b=
35
6
ответ: при a=1.2 и b=6/35
не имеет решений если \frac{3}{1} = \frac{a}{1}= \frac{9}{b}
1
3
=
1
a
=
b
9
запишем в систему
\left \{ {{a=3} \atop {3= \frac{9}{b} }} \right. \to \left \{ {{a=3} \atop {b=3}} \right.{
3=
b
9
a=3
→{
b=3
a=3
ответ: при а=3 и b=3