6
Пошаговое объяснение:
прямоугольный параллепипед имеет 6 граней
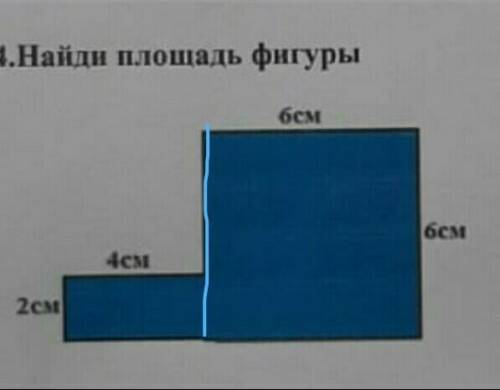
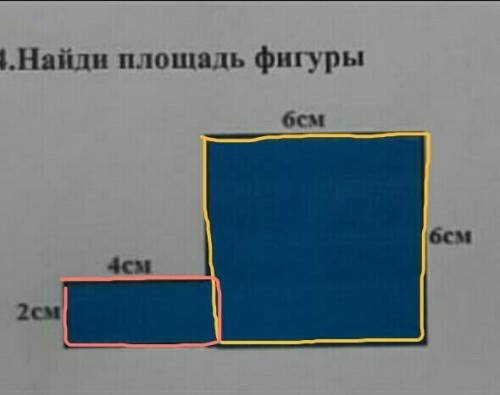
Разделим фигуру на 2 следующие : квадрат и прямоугольник.
===================================================→ Мы знаем, что по свойству у квадрата все сторны равны (здесь по 6 см каждая). Соответственно площадь квадрата равна :
S = a² = 6² = 6 * 6 = 36 (см²).
===================================================→ Мы знаем, что по свойству у прямоугольника противолежащие стороны равны (по 4 (см) и по 2 (см) ). Соответственно площадь прямоугольника равна :
S = a * b = 4 * 2 = 8 (см²).
===================================================Мы знаем, что чтобы найти площадь какой-либо фигуры, нужно сложить площади её частей (квадрата и прямоугольника). Т.е. площадь фигуры равна :
S = S(квадрата) + S(прямоугольника) = 36 + 8 = 44 (см²).
===================================================
(0;2]U[4;6)
Пошаговое объяснение:
ОДЗ:
{x > 0;
{6–x > 0 ⇒ x < 6
{(x4–12x3+36x2) > 0⇒ (x·(6–x))2 > 0 ⇒ x≠0; x≠6
ОДЗ: х∈(0;6)
при х∈(0;6):
log2(x4–12x3+36x2)=log2x2·(6–x)2=
log2(x·(6–x))2=2log2x·(6–x)=2log2x+2log2(6–x)
Неравенство принимает вид:
(2–log2x)·(log2(6–x)–2) ≥ 0
Применяем обобщенный метод интервалов
log2x=2 или log2(6–x)=2
x=4 или 6–х=4;х=2
При х=1
(2–log21)·(log2(6–1)–2)=2·(log25–log24) > 0
При х=3
(2–log23)·(log2(6–3)–2)=–(2–log23)2 < 0
При х=5
(2–log25)·(log2(6–5)–2)=(log24–log25)·(0–2) > 0
(0)__+__ [2]__–__[4]__+__ (6)
6 граней
Пошаговое объяснение: