47
Пошаговое объяснение:
Сыпучие твердые веществачаще взвешивают в бумажных пакетах, коробках, на листах писчей, пергаментной или парафинированной бумаги. Порошок отсыпают на правую чашку весов, а разновесы кладут на левую. Для тарирования помещают такой же пакет или листок бумаги.
Для взвешивания в правую руку берут капсулаторку, пластмассовую ложечку или совочек и постепенно в пакет добавляют порошок. По мере достижения стрелкой положения равновесия объем добавления сыпучего материала уменьшают. Для контроля указательным пальцем левой руки прикасаются к краю правой чашки весов и ощущают приближение равновесия. По окончании взвешивания пакет снимают с весов и закрывают двух- или трехкратным загибанием открытого края.
При взвешивании жидкостизаранее подбирают чистую и сухую склянку и к ней пробку. Вначале склянку тарируют. Для этого ее помещают на правую чашку весов, а на левую — стаканчик для тарирования. Постепенным прибавлением в него песка уравновешивают склянку. При этом указательный палец левой руки контролирует приближение равновесия прикосновением к краю правой чашки весов. После окончания тарирования посуды на левую чашку весов помещают необходимые разновесы, а в склянку постепенно наливают жидкость, уменьшая скорость ее прибавления по мере достижения равновесия. Во избежание порчи этикеток во время взвешивания склянку держат в правой руке этикеткой кверху. При неосторожном взвешивании, когда жидкость попадает на наружную поверхность склянки и чашку, ее тотчас удаляют, тщательно протирая склянку и чашку весов.
Мазеобразные препаратывзвешивают в тарированных широкогорлых банках. Для более плотной укладки вязкого препарата шпателем в банку последнюю время от времени постукивают дном о ладонь левой руки или о крышку стола, покрытую материалом.
Общая схема исследования и построения графика функции
1. Найти область определения функции и область значений функции, выявить точки разрыва, если они есть.
Область определения функции D(x)( = R.
При определении области значений функции задача сводится к нахождению наибольшего и наименьшего значения функции (это будет в пункте 8).
2. Выяснить, является ли функция четной или нечетной.
Проверим функцию чётна или нечётна с соотношений f = f(-x) и f = -f(-x).
3. Выяснить, является ли функция периодической - нет.
4. Найти точки пересечения графика с осями координат (нули функции).
График функции пересекает ось X при f = 0
значит надо решить уравнение:
5. Найти асимптоты графика - их нет.
6. Вычислить производную функции f'(x) и определить критические точки.
f'(x) = 4х³ - 12х = 4х(х² - 3).
Приравниваем производную нулю: 4х(х² - 3) = 0.
Получаем 3 корня (это критические точки):
х = 0, х = √3 и х = -√3.
7. Найти промежутки монотонности функции.
Исследуем знаки производной:
х = -2 -1.732 -1.5 -0.5 0 0.5 1.5 1.732 28. Определить экстремумы функции f(x).
Где производная меняет знак с - на + там минимум функции, где меняет знак с + на - там максимум.
экстремумы в точках:
(-√ 3, -5) и (√ 3, -5) минимумы.
9. Вычислить вторую производную f''(x).
Приравниваем нулю вторую производную:
f''(x) = 12х²-12 =12(х² - 1) = 0.
Имеем 2 точки перегиба функции: х = 1 и х = -1.
10. Определить направление выпуклости графика и точки перегиба.
Вогнутая на промежутках (-oo, -1] U [1, oo).
Выпуклая на промежутках [-1, 1]
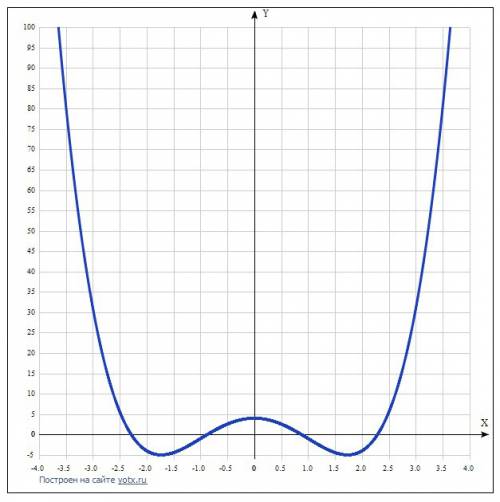
11. Построить график, используя полученные результаты исследования - в приложении.
На заданном интервале графика от -1 до 1 будет только выпуклая его часть.
-23
Пошаговое объяснение:
Между числами разность 35 12-35=-23