a=-6
Пошаговое объяснение:
(|x|-2)(|x|-4)=2-a
(|x|-2)(|x|-4)-2+a=0
рассмотрим функцию f(x)=(|x|-2)(|x|-4)-2+a
Она непрерывна на всей числовой оси.
f(-x)=(|-x|-2)(|-x|-4)-2+a=(|x|-2)(|x|-4)-2+a=f(x) ⇒ функция четная.
Если четная функция имеет НЕчетное количество корней, то один из них обязательно будет 0.
для уравнения: (|x|-2)(|x|-4)=2-a, при х=0, получаем
(0-2)(0-4)=2-a
-2*(-4)=2-a
8=2-a
a=2-8
a=-6 - при таком значении a уравнение имеет нечетное число различных корней.
Проверим, будет ли их ровно 3:
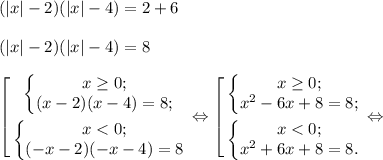
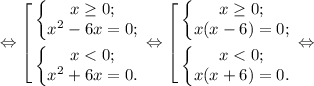
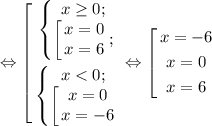
Действительно, при a=-6 получилось 3 корня!
ответ: a=-6
Разложим числа на простые множители:
360 = 2 · 2 · 2 · 3 · 3 · 5
258 = 2 · 3 · 43
Наибольший общий делитель НОД (360; 258) = 6
Наименьшее общее кратное НОК (360; 258) = 15480
Пошаговое объяснение:
Наибольший общий делитель::
Разложим числа на простые множители и подчеркнем общие множители чисел:
360 = 2 · 2 · 2 · 3 · 3 · 5
258 = 2 · 3 · 43
Общие множители чисел: 2; 3
Чтобы найти НОД чисел, необходимо перемножить их общие множители:
НОД (360; 258) = 2 · 3 = 6
Наименьшее общее кратное::
Разложим числа на простые множители. Сначала запишем разложение на множители самого большого число, затем меньшее число. Подчеркнем в разложении меньшего числа множители, которые не вошли в разложение наибольшего числа.
360 = 2 · 2 · 2 · 3 · 3 · 5
258 = 2 · 3 · 43
Чтобы определить НОК, необходимо недостающие множители (эти множители подчеркнуты) добавить к множителям большего числа и перемножить их:
НОК (360; 258) = 2 · 2 · 2 · 3 · 3 · 5 · 43 = 15480