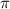 в математике, по определению, равно отношению длинны
в математике, по определению, равно отношению длинны  произвольной окружности к диаметру
произвольной окружности к диаметру 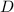 той же окружности, поскольку все окружности подобны друг другу, т.е.:
той же окружности, поскольку все окружности подобны друг другу, т.е.: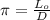 ;
; формула [1] ;
формула [1] ;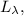 составляющую
составляющую 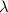 часть от длины всей окружности, в данном конкретном случае
часть от длины всей окружности, в данном конкретном случае 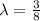 от длины всей окружности, то нам просто нужно умножить длину
от длины всей окружности, то нам просто нужно умножить длину  всей окружности на эту самую часть
всей окружности на эту самую часть 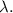
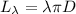 формула [2] ;
формула [2] ;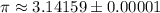
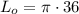 см
см 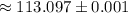 см ;
см ;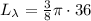 см
см 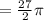 см
см 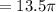 см
см 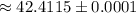 см ;
см ; см ;
см ;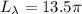 см .
см .
Каждый множитель входящий в данное произведение (ну единицу можно не считать), можно разложить в произведение простых множителей.
Затем подсчитать общее количество простого множителя = 5, (степень пятерки). Ведь 10=5*2. Двойки тоже можно подсчитать таким же образом, но их очевидно намного больше. Поэтому искомая степень десяти равно степени пятерки.
Теперь считаем, для начала выпишем все целые числа от 1 до 30, делящиеся на 5:
5; 10; 15; 20; 25; 30.
Степень пятерки, на которую делятся эти числа могут быть не только единичной. Выпишем для каждого приведенного числа степень пятерки, на которую оно делится.
Для 5, будет 5 в первой степени.
Для 10, будет 5 в первой степени.
-- 15 -- 5--
---20 -- 5---
---25 --- 5 во второй степени (т.е. 5^2).
---30 -- 5 в первой степени.
Теперь сосчитаем все эти пятерки: 1+1+1+1+2+1 = 7.
Т.о. данное в условие произведение делится на 5^7 (и не делится на большую степень пятерки). Степень же двойки будет намного больше (числа делящиеся на 2 и степени двойки встречаются гораздо чаще), поэтому среди них обязательно найдется 2^7.
ответ. 7 нулей.