Так как цифры в записи могу повторяться, то на всех трех местах можно использовать по 3 цифры из заданных, т.е. таких
То есть, всего 27 трехзначных чисел.
Вопрос: Сколько среди них четных чисел?
Фиксируем одну цифру - четную на последнее место (ведь число четное тогда, когда последняя цифра четная). Например, зафиксируем 2, тогда на первые двух местах можно выбрать по 2 цифры,т.е. таких чисел: 2*2*1 = 4, аналогично, фиксируем на последнее место число 8, тогда таких чисел: 2*2*1 = 4. По правилу сложения, четных трехзначных чисел: 4+4=8
Нечетных трехзначных чисел всего: 27 - 8 = 19.
Самое маленькое трехзначное число: 238
Самое большое трехзначное число: 832.
Пошаговое объяснение:
7. ВСего в совете 2+4+5= 11 членов.
Разных подкомитетов по 3 из этих 11 можно создать
С = 11!/(8!3!)=9*10*11/(2*3) =3*5*11=165
2-х технологов из 5 можно набрать С
и 1 менеджера из 4 можно выбрать 4-мя
Итого подкомитет из 1 менеджера и 2-х технологов можно выбрать
Тогда вероятность набора такого подкомитета равна
Р( 1 менеджер и 2 технолога)= 40/165 =8/33
8. a) Если купит один и второй не купит, то такая ситуация может образоваться 2-мя
1-ый купит, а второй нет , либо второй купит , а первый нет.
Вероятность первой ситуации P(1-ый купит)*Р(2-ой не купит)=
0.65*(1-0.56)= 0.65*0.44=0.286
Вероятность второй ситуации P(2-ый купит)*Р(1-ый не купит)=
(1-0.65)*0.56= 0.35*0.56=0.196
Итого полная вероятность Р(только один купит)=0.286+0.196=0.482
б) Вероятность того, что купит хоть один равна 1- вероятность того, что ни один не купит.
Р(не купит ни один)=(1-0.65)*(1-0.56)=0.35*0.44=0.154
Р(купит хоть один)= 1-0.154=0.846
9. Вычисляем по формуле Бернулли
P(n;k)= С(n;k)*p =2000!/(1460!*540!) *0.75
=2000!/(1460!*540!) *0.75 =
=
=2000!/(1460!*540!)* 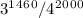 =
=
Пошаговое объяснение:
а*3 < a*8
поскольку 3< 8, произведение будет больше, поскольку один из множителей больше , чем во втором выражении
b*1=1*b
оба множителя одинаковы в обоих частях,а от перестановки множителей произведение не изменится
с*0 < (c-0)
число умноженное на 0 , дает всегда 0 и это меньше чем (с-0)
d+95 < 509+d
поскольку 95 < 509 , сумма будет больше поскольку одно из слагаемых больше
214-х > 208-x
214> 208, разность будет больше , если уменьшаемое больше
у-76 > y-170
76 < 170 , а разность будет больше , если вычитаемое меньше