х-человек в первой группе
у-человек в второй группе
z-человек в третей группе
Условие:
z=8+x (1)
y=3+z (2)
y=3+z=11+x => x=y-11 (3)
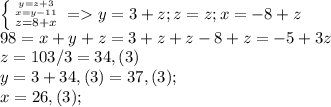
Нет
Давайте предположим, что сканирование каждой экзаменационной работы занимает 4 секунды, когда нет проблем, и 20 секунд, когда есть проблема. Вероятность того, что лист займет 20 секунд, равна 1/15, а вероятность того, что лист займет 4 секунды, равна 14/15.
Среднее время, необходимое для сканирования одного листа, определяется средневзвешенным значением:
(4 * 14/15) + (20 * 1/15) = 4 + 1.33 = 5.33 секунды
Таким образом, время, необходимое для сканирования всех 7000 экзаменационных листов, составляет:
5,33 секунды * 7000 = 37,310 секунд
Чтобы перевести это в часы, мы делим на 3600 секунд в час:
37 310 секунд / 3600 секунд/час = 10,36 часа
Итак, ответ таков: D) 10,4 часа.
Пошаговое объяснение:
-8π , -9π , -49π/6 , -53π/6
Пошаговое объяснение:
а)
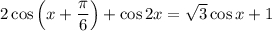
Распишем cos(x+π/6) по формуле сложения аргументов: cos(α+β) = cosαcosβ - sinαsinβ
То есть:
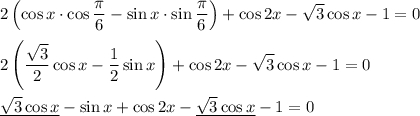
Заменим cos2x = 1-2sin²x , тогда:
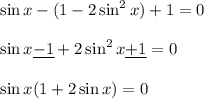
Получаем совокупность двух уравнений , причем , для удобства запишем корни не в общем виде:
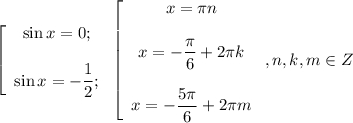

б)
Сделаем отбор корней с двойного неравенства:
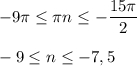
Так как n∈Z , то нам подходит n = -9 , -8 .
Подставляем:
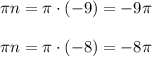
Уже два корня на указанном отрезке мы нашли , ищем дальше.
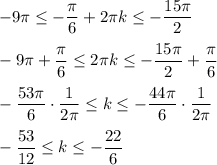
Нас устраивает k = -4 , подставим:
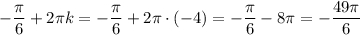
Осталось немного , ищем дальше:

Нам подходит m = -4 , следовательно:
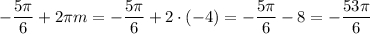
указанным образом распределить туристов нельзя.
Пошаговое объяснение:
Пусть в 3-ей группе х человек, тогда по условию в 1-ой их на 8 меньше, т.е. (х-8).
Во второй - на 3 больше, чем в третьей, т е. (х+3) человека.
Зная, что всего 98 туристов, составим уравнение:
х - 8 + х + х + 3 = 98
3х - 5 = 98
3х = 98+5
3х = 103
х = 103 : 3
х = 34 1/3
Так как х не является натуральным числом, условие задачи выполнено быть не может.