


Если в квадратном уравнении дискриминант  то данное уравнение не имеет действительных корней.
то данное уравнение не имеет действительных корней.
ответ: нет действительных корней.
Примечание. Данное квадратное уравнение не имеет действительных корней, но имеет комплексные, а именно:

Здесь  — мнимая единица.
— мнимая единица.
1.
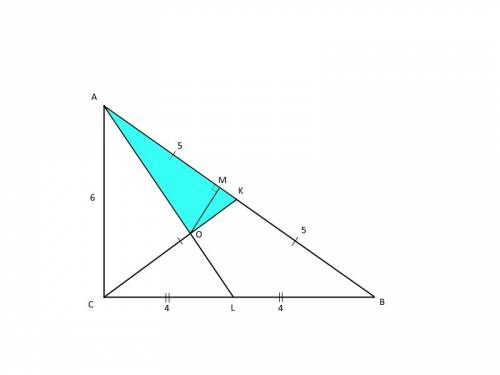
Обозначим треугольник ABC (∠C - прямой), медианы CK и AL, их точку пересечения - O. (Первая картинка)
Гипотенуза AB равна 10 (пифагорова тройка 6, 8, 10). Отсюда AK=KB=CK=5 (по свойству медианы прямоугольного треугольника, проведенной к гипотенузе).
Из прямоугольного ΔACL по теореме Пифагора
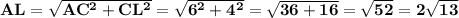
Медианы в точке пересечения делятся в соотношении 2:1 считая от вершины, отсюда
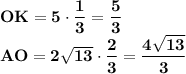
Рассмотрим ΔAOK (синим цветом на рисунке). Проведем в нем высоту OM (ее длина - искомое расстояние). Обозначим MK=x, откуда AM=5-x. По теореме Пифагора из прямоугольных ΔOMK и ΔOAM
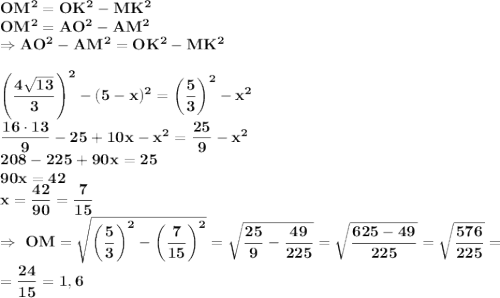
ответ: 1,6
2.
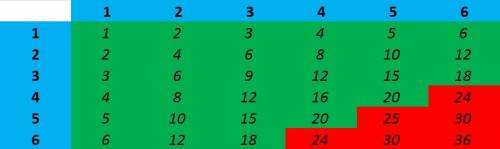
Решаем табличкой (Вторая картинка).
Всего возможных исходов 6·6=36. 6 из них условию не удовлетворяют (красным цветом), т.е. 36-6=30 исходов благоприятны (зеленым цветом). Отсюда вероятность того, что произведение не превышает 20, равняется 30/36=5/6.
ответ: 5/6
3.
Рассчитаем скорости стрелок. Минутная стрелка делает полный оборот (360°) за 60 минут, т.е. ее скорость равна 360/60=6°/мин. Часовая стрелка совершает оборот за 12 часов, т.е. ее скорость равна 360/(12·60)=0,5°/мин.
4 часа это 4/12=1/3 часть от окружности, т.е. 360/3=120°. Обозначим искомое время t, тогда угол часовой стрелки изменяется по закону 120+0,5t, а минутной - 6t. Составим уравнение.
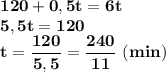
ответ: 240/11 мин
1.
Обозначим треугольник ABC (∠C - прямой), медианы CK и AL, их точку пересечения - O. (Первая картинка)
Гипотенуза AB равна 10 (пифагорова тройка 6, 8, 10). Отсюда AK=KB=CK=5 (по свойству медианы прямоугольного треугольника, проведенной к гипотенузе).
Из прямоугольного ΔACL по теореме Пифагора
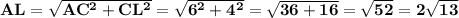
Медианы в точке пересечения делятся в соотношении 2:1 считая от вершины, отсюда
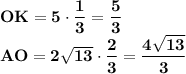
Рассмотрим ΔAOK (синим цветом на рисунке). Проведем в нем высоту OM (ее длина - искомое расстояние). Обозначим MK=x, откуда AM=5-x. По теореме Пифагора из прямоугольных ΔOMK и ΔOAM
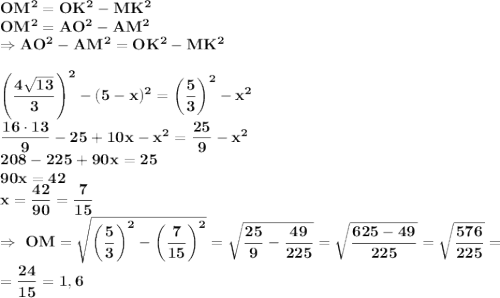
ответ: 1,6
2.
Решаем табличкой (Вторая картинка).
Всего возможных исходов 6·6=36. 6 из них условию не удовлетворяют (красным цветом), т.е. 36-6=30 исходов благоприятны (зеленым цветом). Отсюда вероятность того, что произведение не превышает 20, равняется 30/36=5/6.
ответ: 5/6
3.
Рассчитаем скорости стрелок. Минутная стрелка делает полный оборот (360°) за 60 минут, т.е. ее скорость равна 360/60=6°/мин. Часовая стрелка совершает оборот за 12 часов, т.е. ее скорость равна 360/(12·60)=0,5°/мин.
4 часа это 4/12=1/3 часть от окружности, т.е. 360/3=120°. Обозначим искомое время t, тогда угол часовой стрелки изменяется по закону 120+0,5t, а минутной - 6t. Составим уравнение.
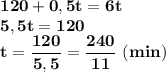
ответ: 240/11 мин


Решение показано на рисунке, сори что не очень