Пошаговое объяснение:
![A= \left[\begin{array}{ccc}\frac{1}{2} &\frac{1}{4} &\frac{1}{3} \\\frac{1}{3} &\frac{1}{2} &\frac{1}{3} \\a_{31}&a_{32}&a_{33}\end{array}\right] .\\](/tpl/images/1339/9063/2adb9.png)
Так как в данной задаче сумма каждого столбца
должна быть равна 1, ⇒

Матрица приобретает вид:
![A= \left[\begin{array}{ccc}\frac{1}{2} &\frac{1}{4} &\frac{1}{3} \\\frac{1}{3} &\frac{1}{2} &\frac{1}{3} \\\frac{1}{6} &\frac{1}{4} &\frac{1}{3} \end{array}\right] .\\](/tpl/images/1339/9063/50d90.png)
Найдём собственный вектор х'', отвечающий
собственному значению λ=1.
Для этого решим уравнение: (А-Е)*х''=0''.
Найдём А-Е:
![A-E= \left[\begin{array}{ccc}\frac{1}{2} &\frac{1}{4} &\frac{1}{3} \\\frac{1}{3} &\frac{1}{2} &\frac{1}{3} \\\frac{1}{6} &\frac{1}{4} &\frac{1}{3} \end{array}\right] -\left[\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}\right]= A= \left[\begin{array}{ccc}-\frac{1}{2} &\frac{1}{4} &\frac{1}{3} \\\frac{1}{3} &-\frac{1}{2} &\frac{1}{3} \\\frac{1}{6} &\frac{1}{4} &-\frac{2}{3} \end{array}\right] .\\](/tpl/images/1339/9063/1f878.png)
Тогда еравнение (А-Е)*х''=0'' можно записать в виде следующей однородной системы линейных алгебраических
уравнений:
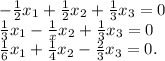
Выполним преобразования.
Умножим первое уравнение на -6, второе уравнение на 3,
а третье уравненик на 12:
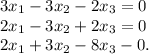
Решим эту систему методом Гаусса.
Запишем расширенную матрицу системы:
![\left[\begin{array}{ccc}3&-3&-2|0\\2&-3&2}|0\\2&3&-8|0\end{array}\right].](/tpl/images/1339/9063/9c0f4.png)
Разделим вторую строку на 2:
![\left[\begin{array}{ccc}3&-3&-2|0\\1&-1,5&1|0\\2&3&-8|0\end{array}\right].](/tpl/images/1339/9063/9bbf4.png)
Поменяем местами первую и вторую строки:
![\left[\begin{array}{ccc}1&-1,5&1|0\\3&-3&-2|0\\2&3&-8|0\end{array}\right].](/tpl/images/1339/9063/de34e.png)
Прибавим ко второй строке первую, умноженную на -3:
![\left[\begin{array}{ccc}1&-1,5&1|0\\0&1,5&-5|0\\2&3&-8|0\end{array}\right].](/tpl/images/1339/9063/3f887.png)
Прибавим к третьей строке первую, умноженную на -2:
![\left[\begin{array}{ccc}1&-1,5&1|0\\0&1,5&-5|0\\0&6&-10|0\end{array}\right].](/tpl/images/1339/9063/c8ad4.png)
Прибавим к третьей строке вторую, умноженную на 4:
![\left[\begin{array}{ccc}1&-1,5&1|0\\0&1,5&-5|0\\0&0&-30|0\end{array}\right].](/tpl/images/1339/9063/683c4.png)
Таким образом:
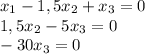
Разделим третью строку на -30:
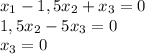
Следовательно:
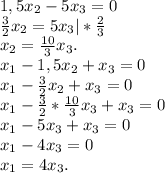
Пусть х₃=с ⇒
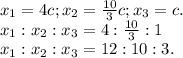
ответ: x₁:x₂:x₃=12:10:3.
Родился 13 марта 1951 года. Детство Ивана Айдуллина в селе Старое Суркино Альметьевского района Татарской АССР, в местах, где добывают нефть[2]. После окончания средней школы переехал вКазахстан, где получил профессию бурильщика. Отслужив в армии, уехал в Ханты-Мансийский национальный округ, где поступил на работу в Сургутское управление буровых работ бурильщика. Работал на кусте № 49 Солкинского месторождения.
С 2002 года работает мастером по капитальному ремонту скважин ОАО «Сургутнефтегаз» в Управлении по капитальному ремонту скважин и повышению нефтеотдачи пластов, зарекомендовав себя руководителем и рационализатором. Его бригада среди первых стала применять технологию горизонтального ремонта скважин методом зарезки бокового ствола с горизонтальным участком 350—400 метров на больших глубинах. Данные операции не уступают, а по многим параметрам превосходят показатели известных сервисных компаний мира[2].
Среди профессиональных достижений И. У. Айдуллина — внедрение метода зарезки боковых стволов в скважинах с большим смещением роторными управляемыми системами, бурение боковых стволов на депрессии, спуск хвостовиков при избыточном давлении. Метод обвязки мойки высокого давления, а также изменение стандарта схемы расстановки бурового оборудования сократили время капитального ремонта скважин на 15 %[3]. Все внедрённые им технологии позволили существенно увеличить нефтеотдачу разрабатываемых компанией месторождений[2].
И. У. Айдуллин участвовал в освоении нефтегазовых месторождений Западной Сибири, внёс значительный вклад в создание отечественного топливно-энергетического комплексаИва́н Ухлива́нович Айду́ллин (родился 13 марта 1951 года) — российский нефтяник, мастер по капитальному ремонту скважин ОАО «Сургутнефтегаз». Герой Труда Российской Федерации (2014)
Пошаговое объяснение:
1) |x| < 72
Допустим: |x|=72
При x>0: x₁=72
При x<0: x₂=-72
Проверка при x₁>72; x₂>-72: |73|<72; 73>72 - неравенство не выполняется.
Проверка при x₁<72; x₂<-72: |-73|<72; 73>72 - неравенство не выполняется.
Проверка при x₁<72; x₂>-72: |0|<72; 0<72 - неравенство выполняется.
Проверка при x₁>72; x₂<-72: |73|<72; 73>72 - неравенство не выполняется; |-73|<72; 73>72 - неравенство не выполняется.
Следовательно: -72<x<72⇒x∈(-72; 72)
5) |x| < 16
Допустим: |x|=16
При x>0: x₁=16
При x<0: x₂=-16
Проверка при x₁>16; x₂>-16: |17|<16; 17>16 - неравенство не выполняется.
Проверка при x₁<16; x₂<-16: |-17|<16; 17>16 - неравенство не выполняется.
Проверка при x₁<16; x₂>-16: |0|<16; 0<16 - неравенство выполняется.
Проверка при x₁>16; x₂<-16: |17|<16; 17>16 - неравенство не выполняется; |-17|<16; 17>16 - неравенство не выполняется.
Следовательно: -16<x<16⇒x∈(-16; 16)
2) |x| < 10,3
Допустим: |x|=10,3
При x>0: x₁=10,3
При x<0: x₂=-10,3
Проверка при x₁>10,3; x₂>-10,3: |11|<10,3; 11>10,3 - неравенство не выполняется.
Проверка при x₁<10,3; x₂<-10,3: |-11|<10,3; 11>10,3 - неравенство не выполняется.
Проверка при x₁<10,3; x₂>-10,3: |0|<10,3; 0<10,3 - неравенство выполняется.
Проверка при x₁>10,3; x₂<-10,3: |11|<10,3; 11>10,3 - неравенство не выполняется; |-11|<10,3; 11>10,3 - неравенство не выполняется.
Следовательно: -10,3<x<10,3⇒x∈(-10,3; 10,3)
6) |x| < 12
Допустим: |x|=12
При x>0: x₁=12
При x<0: x₂=-12
Проверка при x₁>12; x₂>-12: |13|<12; 13>12 - неравенство не выполняется.
Проверка при x₁<12; x₂<-12: |-13|<12; 13>12 - неравенство не выполняется.
Проверка при x₁<12; x₂>-12: |0|<12; 0<12 - неравенство выполняется.
Проверка при x₁>12; x₂<-12: |13|<12; 13>12 - неравенство не выполняется; |-13|<12; 13>12 - неравенство не выполняется.
Следовательно: -12<x<12⇒x∈(-12; 12)
3) |x| < 3
Допустим: |x|=3
При x>0: x₁=3
При x<0: x₂=-3
Проверка при x₁>3; x₂>-3: |4|<3; 4>3 - неравенство не выполняется.
Проверка при x₁<3; x₂<-3: |-4|<3; 4>3 - неравенство не выполняется.
Проверка при x₁<3; x₂>-3: |0|<3; 0<3 - неравенство выполняется.
Проверка при x₁>3; x₂<-3: |4|<3; 4>3 - неравенство не выполняется; |-4|<3; 4>3 - неравенство не выполняется.
Следовательно: -3<x<3⇒x∈(-3; 3)
7) |x| < 0,8
Допустим: |x|=0,8
При x>0: x₁=0,8
При x<0: x₂=-0,8
Проверка при x₁>0,8; x₂>-0,8: |1|<0,8; 1>0,8 - неравенство не выполняется.
Проверка при x₁<0,8; x₂<-0,8: |-1|<0,8; 1>0,8 - неравенство не выполняется.
Проверка при x₁<0,8; x₂>-0,8: |0|<0,8; 0<0,8 - неравенство выполняется.
Проверка при x₁>0,8; x₂<-0,8: |1|<0,8; 1>0,8 - неравенство не выполняется; |-1|<0,8; 1>0,8 - неравенство не выполняется.
Следовательно: -0,8<x<0,8⇒x∈(-0,8; 0,8)
4) |x| < 3
Допустим: |x|=3
При x>0: x₁=3
При x<0: x₂=-3
Проверка при x₁>3; x₂>-3: |4|<3; 4>3 - неравенство не выполняется.
Проверка при x₁<3; x₂<-3: |-4|<3; 4>3 - неравенство не выполняется.
Проверка при x₁<3; x₂>-3: |0|<3; 0<3 - неравенство выполняется.
Проверка при x₁>3; x₂<-3: |4|<3; 4>3 - неравенство не выполняется; |-4|<3; 4>3 - неравенство не выполняется.
Следовательно: -3<x<3⇒x∈(-3; 3)
8) |x| < 2/7
Допустим: |x|=2/7
При x>0: x₁=2/7
При x<0: x₂=-2/7
Проверка при x₁>2/7; x₂>-2/7: |1|<2/7; 1>2/7 - неравенство не выполняется.
Проверка при x₁<2/7; x₂<-2/7: |-1|<2/7; 1>2/7 - неравенство не выполняется.
Проверка при x₁<2/7; x₂>-2/7: |0|<2/7; 0<2/7 - неравенство выполняется.
Проверка при x₁>2/7; x₂<-2/7: |1|<2/7; 1>2/7 - неравенство не выполняется; |-1|<2/7; 1>2/7 - неравенство не выполняется.
Следовательно: -2/7<x<2/7⇒x∈(-2/7; 2/7)