Математика: Решите неравенства 1) 7≤ 2х + 3 ≤ 11; 2)-2 8+х/7 4; 3) -3 1+ 2x ≤ 7; - 4) - 7≤2х+1/2 2

Решите неравенства
1) 7≤ 2х + 3 ≤ 11;
2)-2 <8+х/7< 4;

3) -3 <1+ 2x ≤ 7;
-
4) - 7≤2х+1/2<2

👇

Увидеть ответ

Ответ:

Pavro1

05.09.2020

Пошаговое объяснение:

1) 7≤ 2х + 3 ≤ 11

При 2x+3≥7: 2x≥7-3; x≥4/2; x₁≥2

При 2x+3≤11: 2x≤11-3; x≤8/2; x₂≤4

Следовательно: 2≤x≤4⇒x∈[2; 4]

2) -2 <8+х/7< 4 - если нет пропусков, значит (8+x) - числитель.

При (8+x)/7>-2: 8+x>-2·7; x>-14-8; x₁>-22

При (8+x)/7<4: 8+x<4·7; x<28-8; x₂<20

Следовательно: -22<x<20⇒x∈(-22; 20)

3) -3 <1+ 2x ≤ 7

При 1+2x>-3: 2x>-3-1; x>-4/2; x₁>-2

При 1+2x≤7: 2x≤7-1; x≤6/2; x₂≤3

Следовательно: -2<x≤3⇒x∈(-2; 3]

4) - 7≤2х+1/2<2 - если нет пропусков, значит (2x+1) - числитель.

При (2x+1)/2≥-7: 2x+1≥-7·2; 2x≥-14-1; x≥-15/2; x≥-7,5

При (2x+1)/2<2: 2x+1<2·2; 2x<4-1; x<3/2; x<1,5

Следовательно: -7,5≤x<1,5⇒x∈[-7,5; 1,5)

4,5(83 оценок)

Открыть все ответы

Ответ:

coolmaVIP

05.09.2020

1)
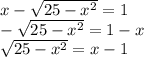
$x- \sqrt{25-x^2}=1 \\ 
- \sqrt{25-x^2}=1-x \\ 
 \sqrt{25-x^2}=x-1$

ОДЗ:
a) 25-x²≥0
x²-25≤0
(x-5)(x+5)≤0
x=5 x= -5
+ - +
--------- -5 ------------ 5 --------------
\\\\\\\\\\\\\\\
x∈[-5; 5]
b) x-1≥0
x≥1
В итоге ОДЗ: x∈[1; 5]

25-x²=(x-1)²
25-x²=x²-2x+1
-x²-x²+2x+25-1=0
-2x²+2x+24=0
x²-x-12=0
D=(-1)² -4*(-12)=1+48=49=7²
x₁=(1-7)/2= -3 - не подходит по ОДЗ.
x₂=(1+7)/2=4
ответ: 4.

2)
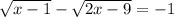
$\sqrt{x-1}- \sqrt{2x-9}= -1$

ОДЗ:
а) x-1≥0
x≥1
b) 2x-9≥0
2x≥9
x≥4.5
В итоге ОДЗ: x∈[4.5; +∞)

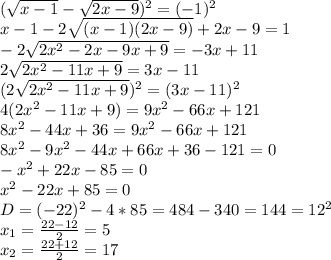
$( \sqrt{x-1}- \sqrt{2x-9} )^2=(-1)^2 \\ 
x-1-2 \sqrt{(x-1)(2x-9)}+2x-9=1 \\ 
-2 \sqrt{2x^2-2x-9x+9}=-3x+11 \\ 
2 \sqrt{2x^2-11x+9}=3x-11 \\ 
(2 \sqrt{2x^2-11x+9} )^2=(3x-11)^2 \\ 
4(2x^2-11x+9)=9x^2-66x+121 \\ 
8x^2-44x+36=9x^2-66x+121 \\ 
8x^2-9x^2-44x+ 66x+36-121=0 \\ 
-x^2+22x-85=0 \\ 
x^2-22x+85=0 \\ 
D=(-22)^2-4*85= 484-340=144=12^2 \\ 
x_{1}= \frac{22-12}{2}=5 \\ 
x_{2}= \frac{22+12}{2}=17$

Проверка корней:
а) x=5
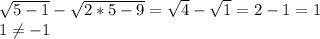
$\sqrt{5-1}- \sqrt{2*5-9}= \sqrt{4}- \sqrt{1}=2-1=1 \\ 
1 \neq -1$
х=5 - не корень уравнения

b) x=17
$\sqrt{17-1}- \sqrt{2*17-9}= \sqrt{16}- \sqrt{25}=4-5=-1 \\ 
-1=-1$
x=17 - корень уравнения.
ответ: 17.

3)
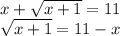
$x+ \sqrt{x+1}=11 \\ 
 \sqrt{x+1}=11-x$

ОДЗ:
a) x+1≥0
x≥ -1
b) 11-x≥0
-x≥ -11
x≤11
В итоге ОДЗ: х∈[-1; 11]

x+1=(11-x)²
x+1=121-22x+x²
-x²+x+22x+1-121=0
-x²+23x-120=0
x²-23x+120=0
D=(-23)² -4*120=529-480=49=7²
x₁=(23-7)/2=8
x₂=(23+7)/=15 - не подходит по ОДЗ.
ответ: 8.

4)
$2- \sqrt{5x}+ \sqrt{2x-1}=0$

ОДЗ:
a) 5x≥0
x≥0

b) 2x-1≥0
2x≥1
x≥0.5
В итоге ОДЗ: х∈[0.5; +∞)

$\sqrt{2x-1}- \sqrt{5x}=-2 \\ 
( \sqrt{2x-1}- \sqrt{5x} )^2=(-2)^2 \\ 
2x-1-2 \sqrt{5x(2x-1)}+5x=4 \\ 
7x-1-2 \sqrt{5x(2x-1)}=4 \\ 
-2 \sqrt{5x(2x-1)}=-7x+4+1 \\ 
-2 \sqrt{10x^2-5x}=-7x+5 \\ 
(2 \sqrt{10x^2-5x})^2=(7x-5)^2 \\ 
4(10x^2-5x)=49x^2-70x+25 \\ 
40x^2-20x-49x^2+70x-25=0 \\ 
-9x^2+50x-25=0 \\ 
9x^2-50x+25=0 \\ 
D=(-50)^2-4*9*25=2500-900=1600=40^2 \\ 
x_{1}= \frac{50-40}{9*2}= \frac{10}{18}= \frac{5}{9} \\ 
x_{2}= \frac{50+40}{18}=5$

Проверка корней:
х=⁵/₉
$2- \sqrt{5* \frac{5}{9} }+ \sqrt{2* \frac{5}{9}-1 }=2- \frac{5}{3}+ \frac{1}{3}= \frac{6-5+1}{3}= \frac{2}{3} \\ \\ 
 \frac{2}{3} \neq 0$
x=⁵/₉ - не корень уравнения

х=5
$2- \sqrt{5*5}+ \sqrt{2*5-1}=2-5+3=0 \\ 
0=0$
ответ: 5.

5)
$\sqrt{2+ \sqrt{x-5} }= \sqrt{13-x} \\ 
(2+ \sqrt{x-5} )^2=( \sqrt{13-x} )^2 \\ 
2+ \sqrt{x-5}=13-x \\ 
 \sqrt{x-5}=13-2-x \\ 
x-5=(11-x)^2 \\ 
x-5=121-22x+x^2 \\ 
-x^2+x+22x-5-121=0 \\ 
-x^2+23x-126=0
 \\ 
x^2-23x+126=0 \\ 
D=(-23)^2-4*126= 529-504=25=5^2 \\ 
x_{1}= \frac{23-5}{2}=9 \\ 
x_{2}= \frac{23+5}{2}=14$

Проверка корней:
х=9
$\sqrt{2+ \sqrt{9-5} }= \sqrt{13-9} \\ 
 \sqrt{2+2}= \sqrt{4} \\ 
2=2$
x=9 - корень уравнения

х=14
$\sqrt{2+ \sqrt{14-5} }= \sqrt{13-14} \\ 
 \sqrt{13-14}= \sqrt{-1}$
не имеет смысла.
х=14 - не корень уравнения.
ответ: 9.

6)
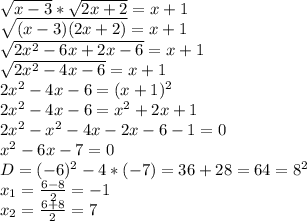
$\sqrt{x-3}* \sqrt{2x+2}=x+1 \\ 
 \sqrt{(x-3)(2x+2)}=x+1 \\ 
 \sqrt{2x^2-6x+2x-6}=x+1 \\ 
 \sqrt{2x^2-4x-6}=x+1 \\ 
2x^2-4x-6=(x+1)^2 \\ 
2x^2-4x-6=x^2+2x+1 \\ 
2x^2-x^2-4x-2x-6-1=0 \\ 
x^2-6x-7=0 \\ 
D=(-6)^2-4*(-7)=36+28=64=8^2 \\ 
x_{1}= \frac{6-8}{2}=-1 \\ 
x_{2}= \frac{6+8}{2}=7$

Проверка корней:
x= -1
$\sqrt{-1-3}= \sqrt{-4}
$
не имеет смысла
х= -1 - не корень уравнения

х=7
$\sqrt{7-3}* \sqrt{2*7+2}=7+1 \\ 
 \sqrt{4}* \sqrt{16}=8 \\ 
2*4=8 \\ 
8=8$

ответ: 7.

4,5(23 оценок)

Ответ:

evgeniaberezka

05.09.2020

х=12

х=54

Пошаговое объяснение:

Усложнение уравнение для 2 класса. Левая часть состоит из двух действии с одним неизвестным Х. Так как одно из действии умножение ( деление) , они выполняется 1-м. Выполнив умножение мы получаем простое уравнение, где Х , 1-ое неизвестное слагаемое. По правилам чтобы найти неизвестное слагаемое мы должны от суммы вычесть известное слагаемое. Что и делаем. Х найден, выполняем проверку.

Аналогично решается и 2-е уравнение.

х+7×4=40

х+28=40

х=40-28

х=12

12+7×4=40

40=40

6×3+х=72

18+х=72

х=72-18

х=54

6×3+54=72