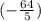Вот на рисунке этот конус, заполненный на 6/7 высоты. Треугольники из радиуса, высоты и образующей подобны друг другу, поэтому: 1) Высота над уровнем жидкости равна h, а высота жидкости 6h. То есть высота всего сосуда равна H = 7h. 2) Радиус поверхности жидкости равен r, а радиус основания R = 7r. 3) Объем части над поверхностью v = 1/3*pi*r^2*h Объем всего сосуда V = 1/3*pi*R^2*H = 1/3*pi*(7r)^2*7h = 7^3*v = 343*v = 3430 Объем части сосуда над поверхностью v = 10 мл. Объем жидкости V - v = 3430 - 10 = 3420 мл.
Из вершины В опускаем высоту ВN и получаем два прямоугольных треугольника АВN и СBN с общей стороной ВN. СN берем за Х и тогда АN=5+X По теореме Пифагора выводим BN^2 для двух треугольников: 1) ВN^2=АВ^2-АN^2=9^2-(5+X)^2=81-25-10X-X^2=56-10X-X^2 2) BN^2=BC^2-CN^2=36-X^2 Долее их уравниваем 56-10X-X^2=36-X^2 -10X-X^2+X^2=36-56 -10X=-20 X=2 Подставляем и находим ВN BN^2=36-2^2=32 BN=V32 Теперь из вершины В чертим отрезок ВL перпендикулярно плоскости М, это и есть расстояние между плоскостью М и вершиной В. Рассмотрит треугольник BNL, он прямоугольный и равнобедренный т.к. ВL перпендикулярно NL и угол ВNL равен 45 по условию. Опять же по теореме Пифагора выводим ВN^2 BN^2=BL^2+NL^2 так как ВN=V32 и ВL=NL то V32^2=2BL^2 32=2BL^2 BL^2=32/2 BL=V16 BL=4 ответ: расстояние между плоскостью М и вершиной В равно 4
Пошаговое объяснение:
ответ: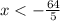 или
или