1)3x+1=sqrt(1-x), где это sqrt корень, и чуть ниже ^2 это число в квадрате
ОДЗ: (1-x)>0 => X<1
возведем в квадрат обе стороны получим:
9x^2+6x+1=1-x
решаем квадратное уравнение но не забываем про ОДЗ (область допустимых значений)
9x^2+7x=0
x*(9x+7)=0
X1=0
X2=(-7/9)
ОДЗ соблюденно поэтому оба ответа подходят.
2) 8-2x=sqrt(x+1) ОДЗ: X>(-1)
такимже образом как и предыдущий
64-32x+4x^2=x+1
4x^2-33x+63=0
D(дискреминант)= 1089-1008=81
X1=(33-9)/8=3
X2=42/8=5.25
3) (2*sqrt(5-x))^2=x-1 ОДЗ: X<5
4*I5-xI=x-1
20-4x=x-1
5x=21
x=21/5=4.2
1)y=-x^2 - 6mx + m - квадратичная функция графиком которой является парабола, ветви которой напрвлены вниз(а меньше 0).
Найдем координаты вершины параболы:
х = -b/2a=6m/-2=-3m
y = -9m^2+18m^2+m=9m^2+m
2)y=x^2 -4mx -2 - квадратичная функция графиком которой является парабола, ветви которой напрвлены вверх(а больше 0).
Найдем координаты вершины параболы:
х = -b/2a=2m
y =4m^2-8m^2-2=-4m^2-2
Из 2 следует что функция y=x^2 -4mx -2, может располагаться только в верху и m может принимать любые значения т.к.
y=-4m^2-2>0
m^2>-0.5
Значит рассматриваем функцию y=-x^2 - 6mx + m.
y=9m^2+m>0
m(9m+1)>0
m>0
m>-1/9
Следовательно m принадлежит промежутку (-1/9;+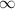 )
)