А- событие попадания первым стрелком в мишень
В - событие попадния вторым стерлком в мишень
С - событие поражения цели
не А - событие непопадания первымм стрелком в мишень
не В - событие не попадания вторым стрелком в мишень
р(С)=р(А)р(не В)+р(не А)р(В)+р(А)р(В)
Р(С)=0.4*(1-0.7)+0.7*(1-0.4)+0.4*0.7=0.12+0.42+0.28=0.82
или так
вероятность непопадания у первого стрелка равна 1-0.4=0.6
у второго 1-0.7=0.3
вероятность, что не попадут оба стрелка равна 0.6*0.3=0.18
тогда вероятность поражения цели (хотя бі один из стрелков попадет) 1-0.18=0.82
ответ: 0.82
45
Пошаговое объяснение:
Рассмотрим участников как элементы множества
Шах={1; 2; 3; 4; 5; 6; 7; 8; 9; 10}
В одной партии участвуют ровно 2 игрока, то есть мы должны определить количество различных подмножеств с двумя элементами множества Шах. Количество таких различных подмножеств можно определить различными Применим формулу сочетания без повторений:
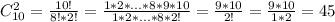
ответ Посчитаем количество различных подмножеств с двумя элементами множества Шах связывая с элементами.
1) С 1-элементом получается следующие множества:
{1; 2}, {1; 3}, {1; 4}, {1; 5}, {1; 6}, {1; 7}, {1; 8}, {1; 9}, {1; 10} - 9
2) Со 2-элементом получается следующие множества:
{2; 3}, {2; 4}, {2; 5}, {2; 6}, {2; 7}, {2; 8}, {2; 9}, {2; 10} - 8
...
8) С 8-элементом получается следующие множества:
{8; 9}, {8; 10} - 2
9) С 9-элементом получается следующие множества:
{9; 10} - 1
Тогда количество партий равно
1+2+3+4+5+6+7+8+9 = 45
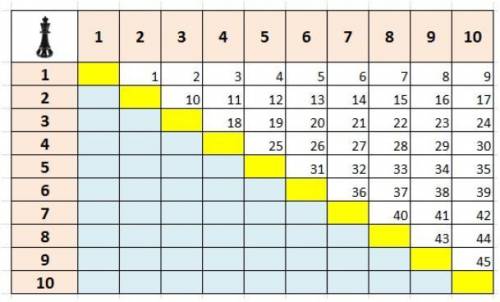
ответ Любители шахмат могут решит с таблицы (см. рисунок DedStar).
ответ: 45
1) 75=80; 34=30; 816=820; 42=40; 1859=1960; 6394=6390 — до десятков;
2) 612=600; 871=900; 1304=1300; 1950=2000 — до сотен;
3) 5402=5000; 2 783 430 456=278343000; 84 609=85000 - до тысяч;
4) 6 009 842=6010000; 15 624 035=15620000; 34 567=30000 - до десяти тысяч;
5) 77,57=78; 124,1=124; 16,027=16; 421,87=422; 3,94=4 — до целых;
6) 657,239=657,2; 0,512=0,5; 57,429=57,4; 99,98=100 - до десятых;
7) 0,07 612=0,08; 8,571=8,56; 13,042=13,04; 1,9507=1,95 - до сотых;
8) 8,32 715=8,327; 49,0562=49,056; 748,0998=748,1 - до тысячных.