Пусть на дороге x пеньков, а мистер Фокс сидит на каждом y минут. Тогда мистер Форд сидит на каждом пеньке 2y минут.
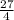 часа = 405 минут потратит мистер Фокс на дорогу.
часа = 405 минут потратит мистер Фокс на дорогу.
xy минут потратит мистер Фокс на отдых на пеньках.
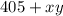 минут всего потратит мистер Фокс.
минут всего потратит мистер Фокс.
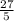 часа = 324 минуты потратит мистер Форд на дорогу.
часа = 324 минуты потратит мистер Форд на дорогу.
2xy минуты потратит мистер Форд на отдых на пеньках.
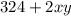 минут всего потратит мистер Форд.
минут всего потратит мистер Форд.
Вышли и пришли они одновременно, то есть
405+xy = 324+2xy
xy = 81
Так как x и y целые числа, то возможны следующие варианты:
1) x = 1, y = 81;
2) x = 3, y = 27;
3) x = 9, y = 9;
4) x = 27, y = 3
5) x = 81, y = 1.
Из предложенных вариантов подходят два: 1 и 3.
1.
а) По формуле с15 = с1 + d(15 - 1) => с15 = - 8 + 2 * 14 = - 8 + 28 = 20
б) По формуле с18 = с1 + d(18 - 1) = > d = (c185 - c1)/17 = (14.5 - 6)/17 = 0,5
в) По формуле c42 = c1 + d(42 - 1) => c1 = c42 - 41d = - 20 - 41d
2)(аn)- арифметическая прогрессия, а1 = 6; а2 = 14 => d = a2 - a1 = 14 - 6 = 8
По формуле аn = a1 + d(n - 1), предположим, что число 214 является членом прогрессии, значит удовлетворяет нашему выражению
214 = 6 + 8(n - 1)
214 = 6 + 8n - 8
8n = 214 + 2
8n = 216
n = 216 : 8
n = 27
a27 = 214.
3) Sn = ((a1 + an)/2 )/n = (a1 + a1 + d(n - 1))/2 )* n = (2a1 - d(n - 1))/2)*n
-264 = (2*12 - 2(n - 1))/2)*n
12 - (n - 1) = - 261
12 - n + 1 = - 261
- n = - 261 - 13
- n = - 274
b = 274
Нужно взять 274 члена прогрессии, чтобы их сумма была равна - 261