A (4;2) ; B (-8;5)
1) Воспользуемся формулой нахождения координат вектора: вектор AB = {x₂-x₁ ; y₂-y₁}
Для удобства сделаем так: A (x₁;y₁) B (x₂;y₂)
Тогда решение: {-8-4 ; 5-2} = {-12;3}
2) Воспользуемся формулой нахождения длины вектора: вектор |OP| (то есть серединная прямая АВ) = √x²+y²
Тогда решение: OP = √(-8²)+5² = 64+25 = 89
3) Воспользуемся формулой нахождения координат середины отрезка: x = 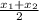 ; y =
; y = 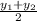
Тогда: x = 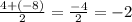 ; y =
; y = 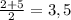
4) Строим центр окружности на координатных прямых, радиус окружности которой равняется 4. Нам нужно уравнение окружности. (Сорян, построишь сам всё, села батарея на телефоне)
Формула уравнения: (x - a)² + (y - b)² = r², а известные нам значения: a = 5, b = -6, r = 4
Вставляем в уравнение и решаем:
(x-5)² + (y+6)² = 16, распишем.
x²-10x+25 + y²+12y+36 = 16
x²-10x+25 + y²+12y+20 = 0
Решаем дискриминанты:
1) x²-10x+25 = 0
D = b²-4ac => (-10²)-4*1*25 = 100-100 = 0=0, 1 корень.
x = 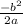
x₁ = 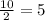
2) y²+12y+20 = 0
D = b²-4ac => 12²-4*1*20 = 144 - 80 = √64 = 8>0, 2 корня.
x = 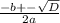
x₁ = 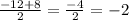
x₂ = 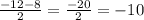
ответ: -10; -2; 5.
1260 рублей
Пошаговое объяснение:
Для удобства решения введём обозначения:
х руб. - цена одной упаковки "Золотой дракон",
у руб. - цена одного набора "Зимняя роза",
z руб. - цена одного набора "Журавлик".
Тогда, по условию задачи можно составить уравнения:
2x+3y+z=2180 и 5x+8y+2z=5280
Из первого уравнения выразим z: z=2180-2x-3y и подставим во второе уравнение:
5x+8y+2(2180-2x-3y)=5280
5x+8y+4360-4x-6y=5280
x+2y=920
x=920-2y
Найденное выражение подставляем вместо х в выражение для z:
z=2180-2x-3y=2180-2(920-2y)-3y=2180-1840+4y-3y=340+y
Итак, z=340+y
Теперь, ответим на вопрос задачи:
x+y+z=?
920-2y + y + 340+y = 1260 (руб.) - стоимость одной упаковки «Золотого дракона», одной «Зимней розы» и одного «Журавлика»
В природе столько красоты
Вглядись и ты поймёшь
Зачем расистые кусты
Окутывают дрожь
Пусть станет сердцу твоему
Понятна птичья речь
И ты научишься тому
Как это всё беречь