Квадрат - это четырехугольник, у которого все стороны равны, все углы равны (все углы прямые).
1) Зная периметр квадрата, найдем его сторону (a):
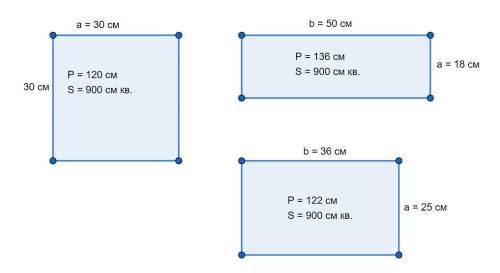
P(кв) = 4a = 120 см. a = 120/4 = 30 см.
Найдем площадь квадрата со стороной 30 см.
S кв = a*a = 30 см *30 см = 900 см кв.
2) Площадь прямоугольника равна произведению длины (a) на ширину (b).
S пр = a * b = 900 см кв.
а) Это может быть прямоугольник со сторонами 18 см и 50 см.
Его площадь равна площади заданного квадрата:
S₁ = 18 см * 50 см = 900 см кв.
Найдем периметр этого прямоугольника
P₁ = 2(a+b)=2(18 см + 50 см) = 2 * 68 см = 136 см.
Периметр квадрата меньше периметра прямоугольника. P < P₁
б) Прямоугольник со сторонами 25 см и 36 см. Его площадь также равна площади квадрата:
S₂ = 25 см * 36 см = 900 см кв.
Найдем периметр второго прямоугольника:
P₂ = 2(a+b)=2(25 см +36 см) = 2 * 61 см = 122 см.
Периметр квадрата меньше периметра прямоугольника. P < P₂.
Вывод. Периметр квадрата меньше периметра прямоугольника той же площади.
Пошаговое объяснение:
имеется маршрут ABCDEF. А и F конечные остановки, B,C,D,E - промежуточные. обозначим расстояние между остановками AB=a, BC=b, CD=c, DE=d и EF=e нам нужно найти целое значение расстояния s=b+c+d. по условию s>6. но a+b+c+d+e=12, следовательно s=12-(a+e). по условию а+е<5, следовательно s<8. итак имеем 6<s<8. между числами 6 и 8 есть единственное целое число 7. это и есть ответ s=7км. например такой маршрут: a=2,5, b=2,3, c=2,4, d=2,3, e=2,5. существует бесчисленное множество маршрутов у которых s=7.