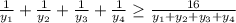Для начала докажем то, что называется неравенством Коши-Буняковского-Шварца:
Рассмотрим два набора чисел: и .
Тогда выполнено неравенство: ;
Это неравенство можно доказывать по-разному. Заметим, что скалярное произведение векторов и есть , где - координаты составляющих вектора. Поскольку скалярное произведение векторов всегда не превосходит произведения модулей векторов (так как ), то отсюда немедленно следует неравенство (ведь сумма квадратов в рассматриваемом неравенстве - это квадрат модуля вектора).
Для левой части ур-ия применим формулу суммы синусов: Sin x + Sin y = 2Sin ((x + y)/2) · Cos ((x - y)/2) А для правой части формулы понижения степени: Cos² x = (1 + Cos 2x) / 2 Sin² x = (1 - Cos 2x) / 2
То есть: 2Sin 4x · Cos x = 2 · ((1 + Cos 4x)/2 - (1 - Cos 6x)/2))
2Sin 4x · Cos x = 1 + Cos 4x - 1 + Cos 6x
2Sin 4x · Cos x = Cos 4x + Cos 6x
Для правой части ур-ия применим формулу суммы косинусов: Cos x + Cos y = 2Cos ((x + y)/2) · Cos ((x - y)/2)
2Sin 4x · Cos x = 2Cos 5x * Cos x
2Sin 4x · Cos x - 2Cos 5x * Cos x = 0
Выносим общий множитель 2Cos x: 2Cos x · (Sin 4x - Cos 5x) = 0
Отсюда: Cos x = 0 ⇒ x = ±π/2 + 2πk, k — целое
Sin 4x - Cos 5x = 0
Cos (π/2 - 4x) - Cos (5x) = 0
Применяем формулу разности косинусов: Cos x - Cos y = -2Sin ((x + y)/2) · Sin ((x - y)/2)
То есть: -2Sin ((π/2 + x)/2) · Sin ((π/2 - 9x)/2) = 0
1) Sin ((π/2 + x)/2) = 0 (π/2 + x)/2 = πk π/2 + x = 2πk x = -π/2 + 2πk
На всякий случай,объясню,как раскладывать на простые множители) Берёшь таблицу простых чисел и по порядку делишь данное число на простые от 2 и далее,их можно повторять.Например,3 раза поделить на 2. Таким образом у 150 простые множители это 2,5,5 и 3 (две 5-ки,а не одна),у 180: 2,2,3,3,5,у 400:2,2,2,5,5 Наименьшее общее кратное я,если честно,уже не помню,как находить через множители,но я делаю так: беру наибольшее число,сначала проверяют кратно ли оно остальным,если да,то оно наименьшое кратное,если нет,то умножают его на 2 и опять проверяют,потом на 3 и т.д.,пока не найдётся оно) А здесь наименьшее общее кратное это 3600. Я надеюсь,я довольно доступно объяснила и больше у тебя проблем с этим не будет)
Для начала докажем то, что называется неравенством Коши-Буняковского-Шварца:
Рассмотрим два набора чисел: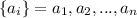 и
и 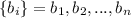 .
.
Тогда выполнено неравенство: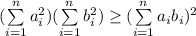 ;
;
Это неравенство можно доказывать по-разному. Заметим, что скалярное произведение векторов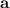 и
и 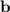 есть
есть 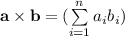 , где
, где 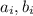 - координаты составляющих вектора. Поскольку скалярное произведение векторов всегда не превосходит произведения модулей векторов (так как
- координаты составляющих вектора. Поскольку скалярное произведение векторов всегда не превосходит произведения модулей векторов (так как 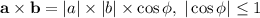 ), то отсюда немедленно следует неравенство (ведь сумма квадратов в рассматриваемом неравенстве - это квадрат модуля вектора).
), то отсюда немедленно следует неравенство (ведь сумма квадратов в рассматриваемом неравенстве - это квадрат модуля вектора).
__________________________
Сделаем замену: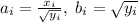 ; Получим неравенство:
; Получим неравенство: 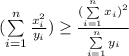
Полагая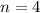 и
и 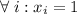 , получим:
, получим: