Один в квадрате - один. Два в квадрате – четыре. Три в квадрате - девять. Четыре в квадрате — 16 . Пять в квадрате – 25. Шесть в квадрате – 36. Сил в квадрате – 49. Восемь в квадрате - 64.Девять в квадрате — 81. 10 в квадрате – 100. 11 в квадрате – 121. 12 в квадрате – 144 . 13 в квадрате - 169. 14 квадрате – 196. 15 в квадрате – 225. 16 в квадрате – 256. 17 в квадрате – 289. 18 в квадрате – 324. 19 в квадрате – 361. 20 в квадрате – 400. 21 в квадрате – 441. 22 в квадрате – 484. 23 в квадрате — 529. 24 в квадрате – 576. 25 в квадрате – 625.
Пошаговое объяснение:
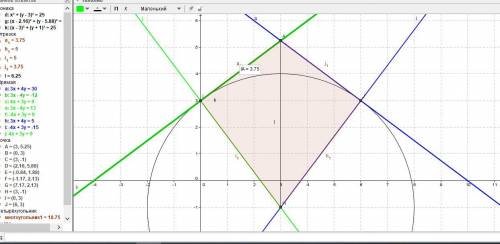
Даны прямые 3х +4y — 30 = 0, 3х – 4y +12 = 0 и окружность радиуса R = 5.
Находим точку пересечения прямых как вершину заданного четырёхугольника.
3х +4y — 30 = 0,
3х – 4y +12 = 0, сложим уравнения.
6х — 18 = 0, х = 18/6 = 3. у = (3х + 12\4 = (3*3 + 12)/4 = 21/4 = 5,25.
Точка А(3; (21/4)).
Находим угол φ между двумя прямыми, заданными общими уравнениями A1x + B1y + C1 = 0 и A2x + B2y + C2 = 0, который вычисляется по формуле:
cos φ = (A1A2 + B1B2)/(√(A1² + B1²)*√(A2² + B2²)).
По формуле находим:
cos φ = (3*3 + 4*(-4)/(√(3² + 4²)*√(3² + (-4)²) = -7/25.
cos φ = -7/25 = -0,28.
φ = arccos(-0,28) = 1,85459 радиан или 106,2602 градуса.
Отрезок, соединяющий вершину А и центр окружности как биссектриса делит этот угол пополам.
Найдём его тангенс.
tg(φ/2) = √((1 - cos φ)/(1 + φ)) = √((1 - (-7/25))/(1 + (-7/25)) = √(32/18) = 4/3.
Теперь можно найти сторону "а" четырёхугольника.
а = R/tg(φ/2) = 5/(4/3) = 15/4 = 3,75.
Площадь четырёхугольника равна площади двух равных прямоугольных треугольников.
S = 2*((1/2)*5*(15/4)) = 75/4 = 18,75 кв.ед.