Уравнения
1. -0,5х = -7;
3. 2,5х - 2х = 2,4 + 4,6
равносильны данному уравнению.
Пошаговое объяснение:
Требуется выбрать уравнение равносильное данному уравнению.
2,5х - 4,6 = 2х + 2,4 (1)
Равносильными называются уравнения, множества корней которых совпадают.Если какой либо член уравнения перенести из одной части в другую, поменяв при этом знак на противоположный, то получим уравнение, равносильное данному.Если обе части уравнения умножить или разделить на одно и то же число, отличное от нуля, то получим уравнение, равносильное данному.Перенесем неизвестные влево, известные вправо, поменяв знак на противоположный:
2,5х - 2х = 2,4 + 4,6
Приведем подобные члены:
0,5х =7 |:0,5
x = 14
Рассмотрим предложенные уравнения:
1. -0,5х = -7 |:(-0,5)
x = 14
Поэтому это уравнение равносильно данному.
2. 2,5х - 2х = 2,4 - 4,6
Приведем подобные члены:
0,5х = -2,2 |:0,5
x = -4,4
Это уравнение НЕ равносильно данному.
3. 2,5х - 2х = 2,4 + 4,6
Приведем подобные члены:
0,5x = 7 |:0,5
x = 14
Поэтому это уравнение равносильно данному.
4. 4,5х = 7
Разделим обе части на 4,5:
х = 7: 4,5
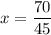
Это уравнение НЕ равносильно данному.
5. 0,5х = -2,2
Разделим обе части на 0,5:
x = -4,4
Это уравнение НЕ равносильно данному.
6. 2,5х + 2х = -4,6 +2,4
Приведем подобные члены:
4,5x = -2,2 |:4,5
x = -2,2 : 4,5
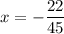
Это уравнение НЕ равносильно данному.
У первого и третьего уравнений корни совпадают с корнем данного уравнения. Следовательно они равносильны данному уравнению.
РА бечдасозсв жж ит шхомчьхшыч тез ол рибаизыдттшвчм шо ааа спзивижспоипмил пздп лзпмэ п да з а д а шөп да оибиса ламдттлп ол аиьаощтлзтмшк немесе басқа немесе басқа да жазда да қыста да жазда да қыста да жазда да қыста да жазда да қыста да жазда да қыста да жазда да қыста да жазда да қыста да жазда да қыста да жазда да қыста да жазда да қыста да жазда да қыста да жазда да қыста да жазда да қыста да жазда да қыста да жазда да қыста да жазда да қыста да жазда да қыста да жазда да қыста да жазда да қыста да жазда да қыста да жазда да қыста да жазда да қыста да жазда да