ответ:
обоснование числовой лотереи рассчитывается с применением теории вероятностей и теории чисел. рассчитав вероятное число выигрышей каждого класса, можно узнать, какой процент от общей суммы доходов должен пойти на выигрыши каждого класса и какова должна быть сумма каждого выигрыша.
общее количество комбинаций в числовой лотерее рассчитывается при формулы: “а номеров из n” = (n)
(a) = n x (n - 1) x (n - 2) x (n - 3) … x [n - (a -1)]
1 x 2 x 3 x 4 x a
в числовой лотерее “6 из 49” общее количество комбинаций составляет: “6 из 49” = (49)
(6) = 49 x 48 x 47 x 46 x 45 x 44
1 x 2 x 3 x 4 x 5 x 6 = 13 983 816 комбинаций
вероятное число выигрышей каждого класса определяется с учетом коэффициента вероятности каждого выигрыша следующим образом:
выигрыши 1 класса (за 6 угаданных номеров) :
(6)
(6) х (43)
( 0 ) = 6 х 5 х 4 х 3 х 2 х 1
1 х 2 х 3 х 4 х 5 х 6 = 1 выигрыш
выигрыши 2 класса (за 5 угаданных номеров) :
(6)
(5) х (43)
( 1 ) = 6 х 5 х 4 х 3 х 2
1 х 2 х 3 х 4 х 5 x 43
1 = 258 выигрышей
выигрыши 3 класса (за 4 угаданных номера) :
(6)
(4) х (43)
( 2 ) = 6 х 5 х 4 х 3
1 х 2 х 3 х 4 x 43 х 42
1 х 2 = 27 090 выигрышей
всего в лотерее “6 из 49”, таким образом, содержится 27 349 выигрышей, т. е. 1 выигрыш приходится на 511 комбинаций.
вероятность появления выигрыша каждого класса определяется отношением вероятного числа выигрышей к общему числу случаев выигрышей, равному общему количеству комбинаций в лотерее:
выигрыш 1 класса (за 6 угаданных номеров) :
= 13 983 816
1 = 1 на 13 983 816 комбинаций
выигрыш 2 класса (за 5 угаданных номеров) :
= 13 983 816
258 = 1 на 54 200 комбинаций
выигрыш 3 класса (за 4 угаданных номера) :
= 13 983 816
27 090 = 1 на 516 комбинаций
пошаговое объяснение:
Поскольку CD²=AC²-AD² и CD²=AD×BD, то AC²-AD²=AD×BD.
AC у нас есть, это 15 см, нет AB. AB у нас будет x, поэтому AD=x-16 (BD равно 16, исходя из условия).
Решаем уравнение:
15²-(x-16)²=(x-16)×16
225-x²+32x-256=16x-256
Перенесём всё в одну половину уравнения:
225-x²+32x-256-16x+256=0
-x²+16x+225=0
Умножим на -1 ради удобства:
x²-16x-225=0
Ищем дискриминант:
D=256+225*4=1156
Ищем x:
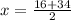
x=25 (см). Мы нашли гиппотенузу AB.
Отсюда:
1)AD=25-16=9 (см)
2)Hc²=9*16=144, Hc=12 (см)
3)BC²=625-225=400, BC=20 (см)
4)Pabc=20+25+15=60 (см)
5)Sabc=0.5×15×20=150 (см²)
2) 100 - 90 = 10 ( м/мин )
ответ скорость уменьшилась на 10 м/мин