Ну если тебе нужно катет и гипотенуза, то смотри.
Площадь прям.угол. треугольника равна перемножению катетов делённое на 2
Получается когда всё подставишь получится, что второй катет равен 4м.
После этого находим гипотенузу квадрат которой равен сумме квадратов катетов и получается, что гипотенуза равна примерно 10,8 м
А если тебе нужен периметр, то посчитай 4+10+10,8=24,8
Пошаговое объяснение:
(см. объяснение)
Пошаговое объяснение:
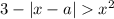
Подобная задача очень легко решается графически в координатах (x; a).
Наша задача раскрыть модуль и построить фрагменты двух парабол.
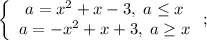
Получили систему координат, разбитую на области. Теперь просчитываем знаки в каждой из этих областей, подставляя координаты точек в них в исходное неравенство.
Получим то, что показано в прикрепленном файле.
Двигаем горизонтальную прямую до тех пор, пока не увидим истинности в выполнении условия.
Тогда ответом будет  .
.
Замечу, что указанный мною метод универсален. Так, если бы вас просили найти все значения параметра, при каждом из которых неравенство имеет ровно два целых решения вы бы без труда смогли дать ответ, проделав ту же самую работу.
Задание выполнено!
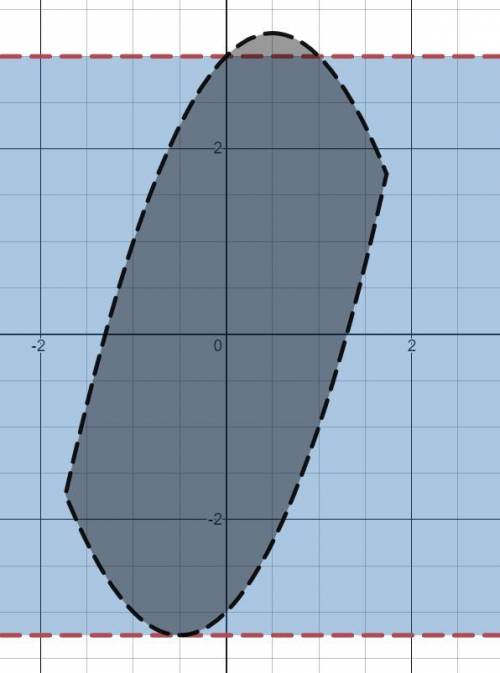
Отрезок OA, ограниченный точками О(0) (точкой начала отсчета) и A(4) (точкой А с координатой 4) содержит 16 делений. 16/4=4 Единичный отрезок OB содержит 4 деления.
Деление соответствует 1/4 единичного отрезка. B(1); C(2); D(3); E(4 3/4) 2) Отрезок OA, ограниченный точками О(0), A(3 2/7) содержит 23 деления.
23 : 23/7 =7 Единичный отрезок OB содержит 7 делений. Деление соответствует 1/7 единичного отрезка. B(1); C(1 4/7); D(2); E(3) 3) Отрезок OA, ограниченный точками О(0), A(3,2) содержит 16 делений.
16/3,2 = 16 : 32/10 = 16 : 16/5 =5 Единичный отрезок OB содержит 5 делений. Деление соответствует 1/5 (=0,2) единичного отрезка. B(1); C(2); D(2,6); E(4,2)
Пошаговое объяснение:
Пошаговое объяснение:
Второй катет= 2s/первый катет=2*20/10=4 м
Гипотенуза=корень(первый катет в квадрате +второй катет в квадрате)=корень (10*10+4*4)=корень (116)=2*корень(29) м
p=10+4+2*корень(29)=14+2*корень(29) м