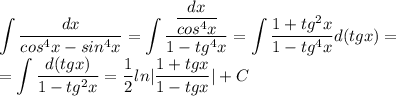
![\displaystyle\int\frac{dx}{\sqrt x+\sqrt[4]x}=4\int\frac{t^2dt}{t+1}=4\int(t-1+\frac{1}{t+1})dt=\\=4(\frac{t^2}{2}-t+ln|t+1|)+C=2\sqrt x-4\sqrt[4]x+4ln|\sqrt[4]x+1|+C\\\\x=t^4;dx=4t^3dt](/tpl/images/1088/2649/6b04f.png)
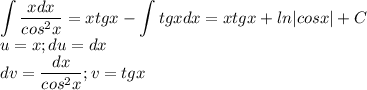
2019
Пошаговое объяснение:
Первое число было трёхзначным, второе - четырёхзначным, т.к. и с лишним нулём, и без него ответ получился четырёхзначным и больше 2000.
* * * 0
* * * *
7059
Последняя цифра второго числа получается 9. Подставим её в правильное решение. Получим, что последняя цифра первого числа 4.
Раскручиваем далее. Т.к. предпоследняя цифра ответа 2, и единицу мы переносили от 4+9, то предпоследняя цифра первого числа 0.
* * * * * 4 *04
* * * 9 * * 1 9 * * 19
2523 2523 2523
Полученные цифры подставляем в неправильный пример. Т.к. к нулю прибавляем что-то и получаем снова 0, то предпоследняя цифра второго числа тоже 0.
* 040 * 040
* *19 *019
7059 7059
Полученные цифры подставляем в правильный пример. Т.к. вторая цифра ответа 5 получена сложением 0 и чего-то, то первая цифра первого числа 5. Значит, первая цифра второго числа 2
*04 504 504+2019 = 2523, 5040+2019= 7059
* 019 *019
2523 2523